This is a series showing Great Circles in Octahedral and Icosahedral symmetries. Circles are indicated by vertices of 60-gons. This first model corresponds to the explanation offered in this article:

Originally the model below was made by David Hall, titled Three-60gons-in-30gon-field. In response to a query about a related construction someone had posted elsewhere, David devised a method for reflecting one of these 60-gons and copying it so as to intruduce Icosahedral Symmetry and Octahedral Symmetry in 30-gon field. This method inspired me to build a series of models with great circles that correspond to structures I had previously made from wire. In these physical models, planes are composed of circles, woven together symmetrically so that there is structural integrity. These are not rigid, but flexible and, depending on certain parameters of construction, transformable art objects that display symmetry. Originals of these date from late 1960s.

For more about this four plane construction, see this model;
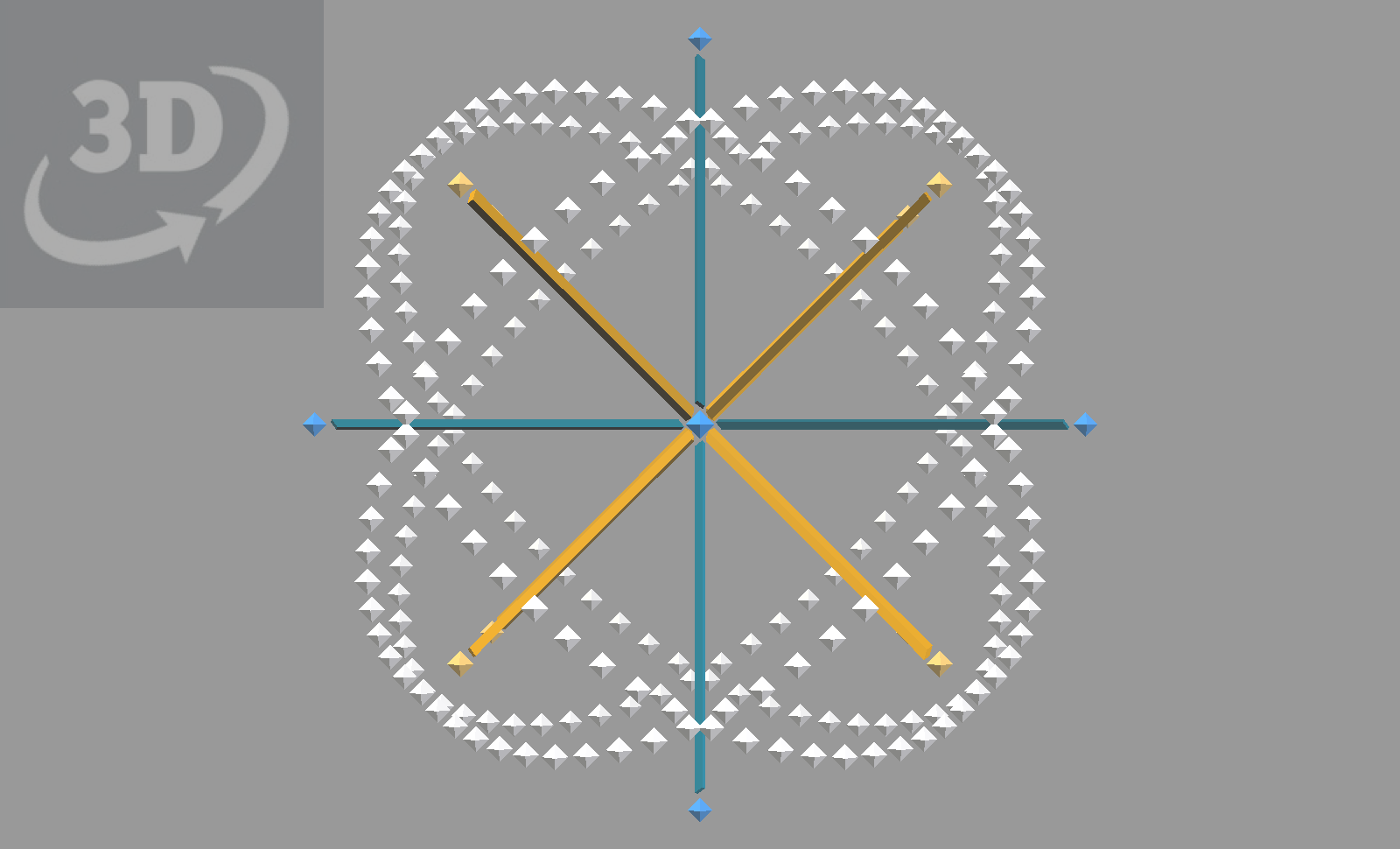
6 60-gons showing 6 axes normal to planes.
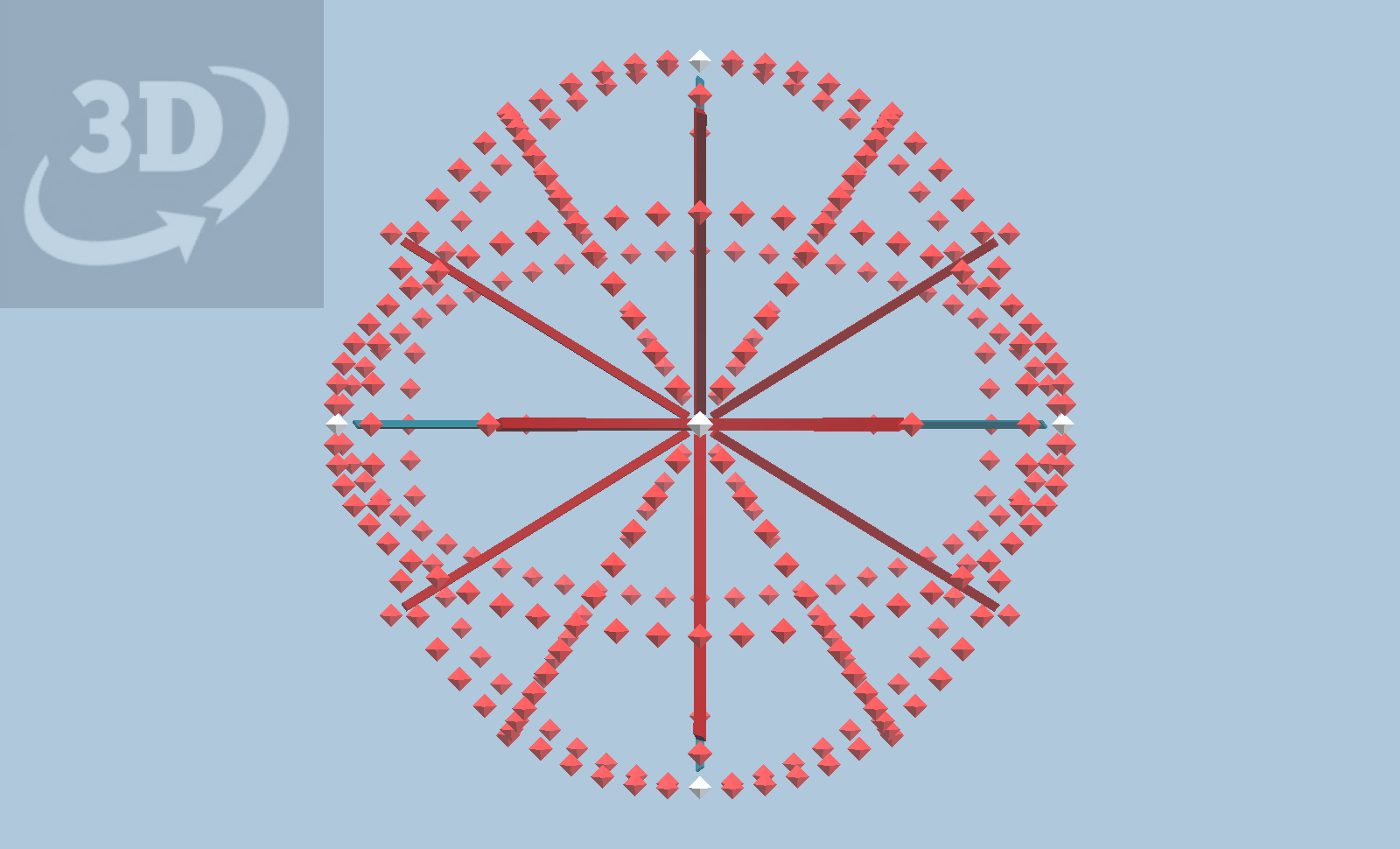
10 60-gons

Combining Six and Ten into 16 60-gon model.
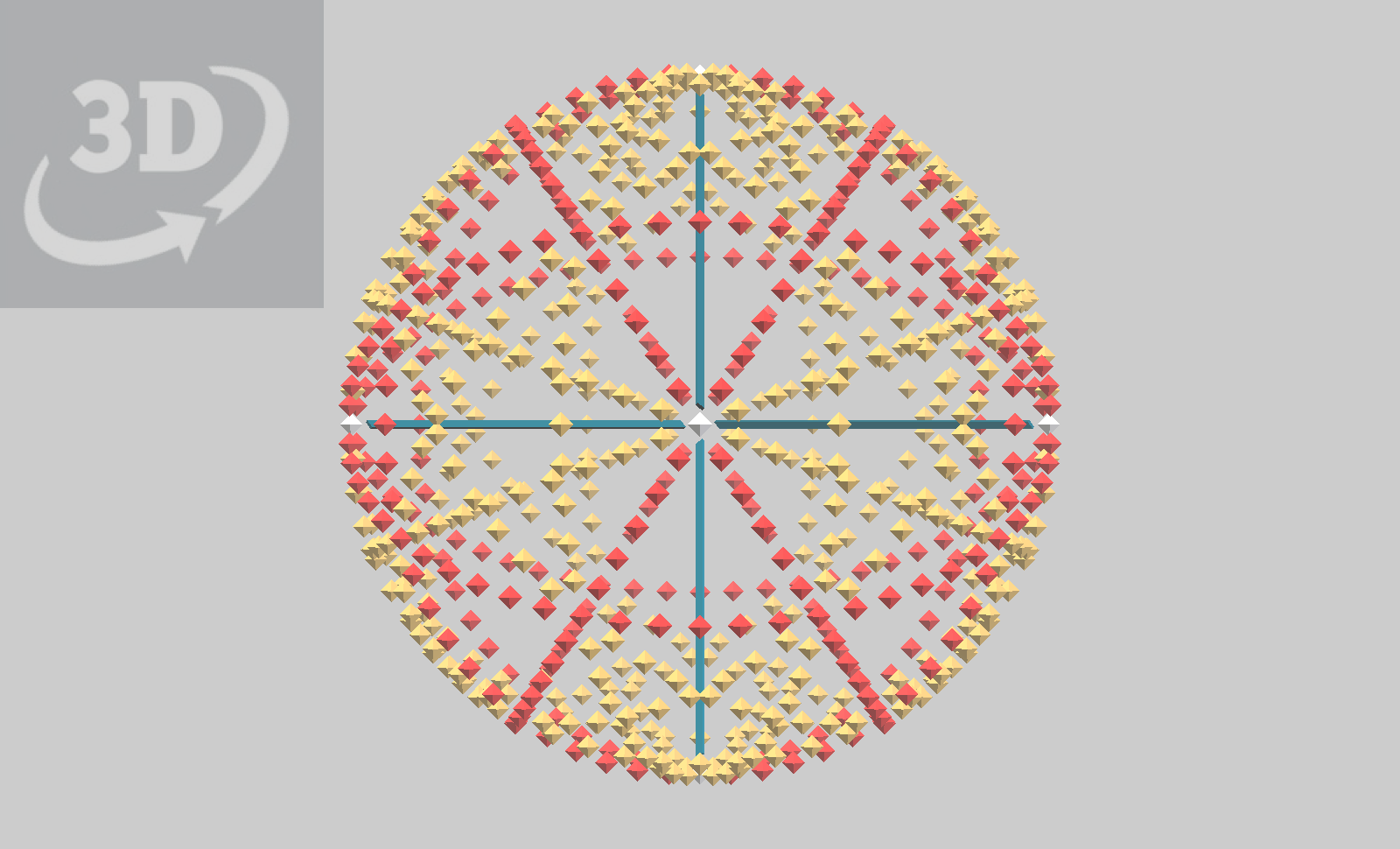
This is the original 3 60-gons copied by reflection to 5 sets of 3, indicating 15 great circles. On desktop, there are several titled Bookmarks which show all Platonic polyhedra, inscribed into the sphere indicated by the 15 60-gons. One also shows a true Geodesic! Note that the vertices of Icosahedron and Dodecahedron are color coded to match red and yellow axes (orbits.) In all these models,the orbit struts are adjusted to be the same length, as radii of a sphere. Note also that while all the Platonic solids are represented, not all possible orientations of them are. There are, for example, 5 ways to orient a cube in icosahedral symmetry. Note that there are 2 Bookmarks for tetrahedra inscribed in the cube, both together making a stellated octahedron.

All above models combined indicate the 31 intersecting planes.