Domes can be constructed in various ways with vZome. Geodesic Domes are mostly defined and/or built with icosahedral symmetry, like this pentakis dodecahedron with all vertices equidistant from center.

However, by a broader definiotion of geodesic, octahedral symmetry is also valid. Given that anything constructed of straight line edges and flat panels can have all vertices lying on a spherical or other curving surface, this model is geodesic in octahedral symmetry, which is to say, arcs passing through sets of vertices that, in this case, are equidistant from a center point meet the definition.

Many domes have been built throughout history, with spherical form, typically with a polar axis, similar to this.

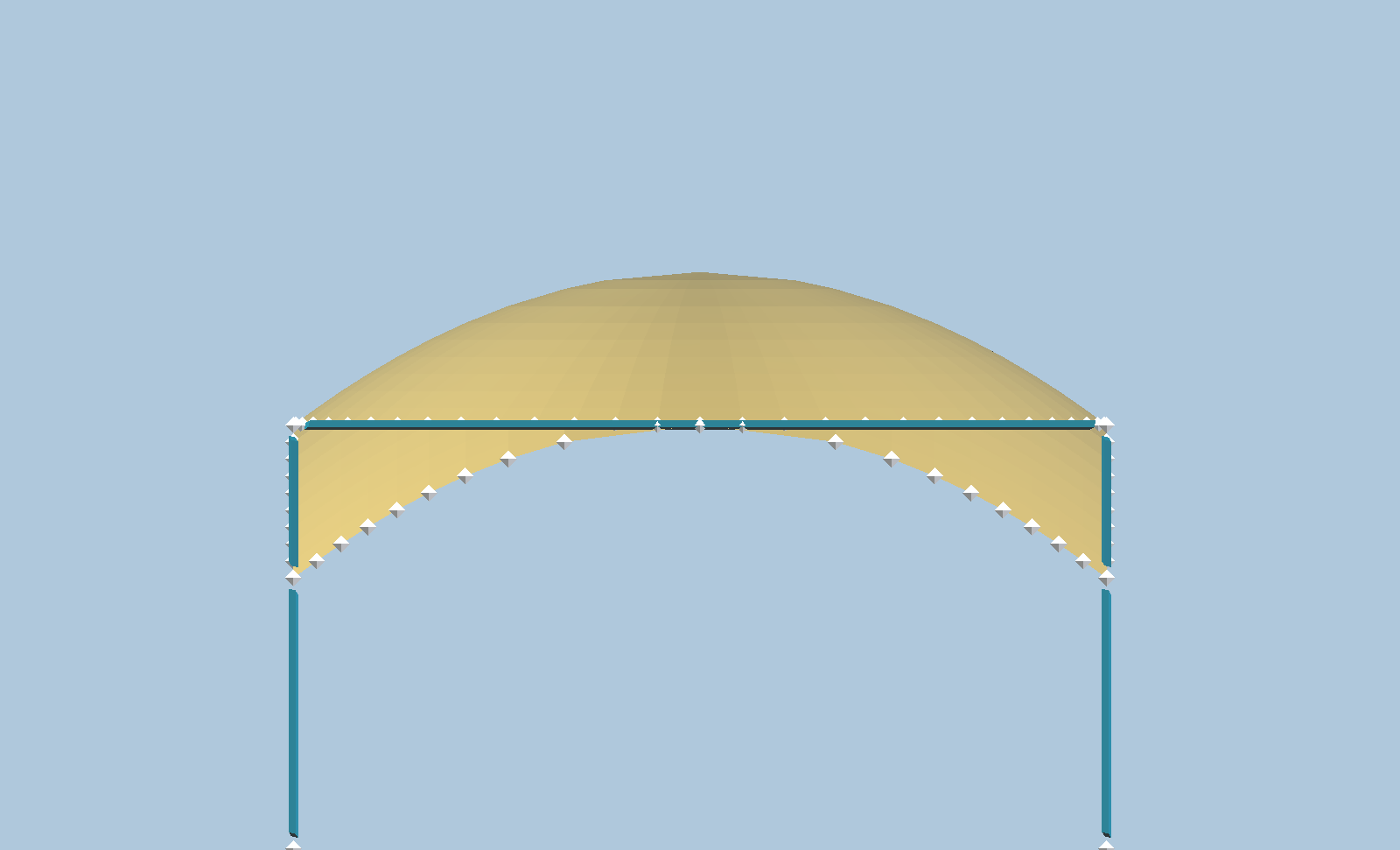
While many are grand scale, construction of smaller scale domed roofs has been widely practiced since antiquity. This is a parabolic form, with the portions of the curve that intersect the cube frame representing outlines of squinches, or structures that carry support from walls to the circular base of the dome. Notably, Hassan Fathy used traditional mud block construction of domes and vaulted roofs.
Geodesic domes are certainly impressive and inspiring. In my explorations of them, though, I became aware of some of the limitations and disadvantages of their application for habitation. In this article, there is a critique of these limitations, which I find accurate. I would add, though, that one aspect that can address some of the issues mentioned is orientation. Many domes I have seen are oriented with a fivefold axis as vertical. By orienting with a 2-fold axis as vertical, it becomes easier to integrate with more standard xyz coordinated structures and plans, and more natural to inhabit. We do, after all, have an anatomy that is 2-fold, or bilateral, with paired hands, eyes, a front and back, up and down, etc. This model is an example of how a geodesic form can be adjoined with a conventional kind of building that facilitates partitioning for amenites, utility spaces, etc., and allows for window selection and placement to be more standard. This particular interior surface of the dome accomodates insulation, wiring, and relative ease of finishing.

From these and other considerations about domes, over time I developed a system for layout and building of frameworks that define spheres. This uses grids in cartesian coordinates where x, y, and z grid point values are √n. This shows an indicated hemisphere in octahedral symmetry. Note that not all struts are filled in. This is a design parameter.

Spherical domes are elegant, and have a certain celestial association. However, this constraint does not make them optimal for living spaces, as has been noted. The √n grid system can be readily adapted to forms like this, which is an Elliptical Ellipsoid. This illustrates several features of this kind of plan. Because of the composition of curved lines in horizontal and vertical planes, the dome can be truncated to build walls with doors, or to merge with adjacent structures. The footprint can be adjusted to meet lot criteria. Partitions can be built within the dome, and floors can be built, aligned with framework. In this model, the frame is shown as planar elements that couple to each other in triple groups, forming a bridgework of structural integrity between an inner surface and the outer hull.

It became apparent to me that this layout system could be applied in a whole range of Quadric surface constructions, such as paraboloids, hyperboloids, as well as ellipsoids. This model shows a simplified framing for an Elliptical Paraboloid, such as can be built with standard materials and tools. Apart from the frame is shown a sample of how an arch is composed from a straight board, cut to a parabola line and recombined. Scenes shows an elliptical section plane

Some other related models can be viewed here.