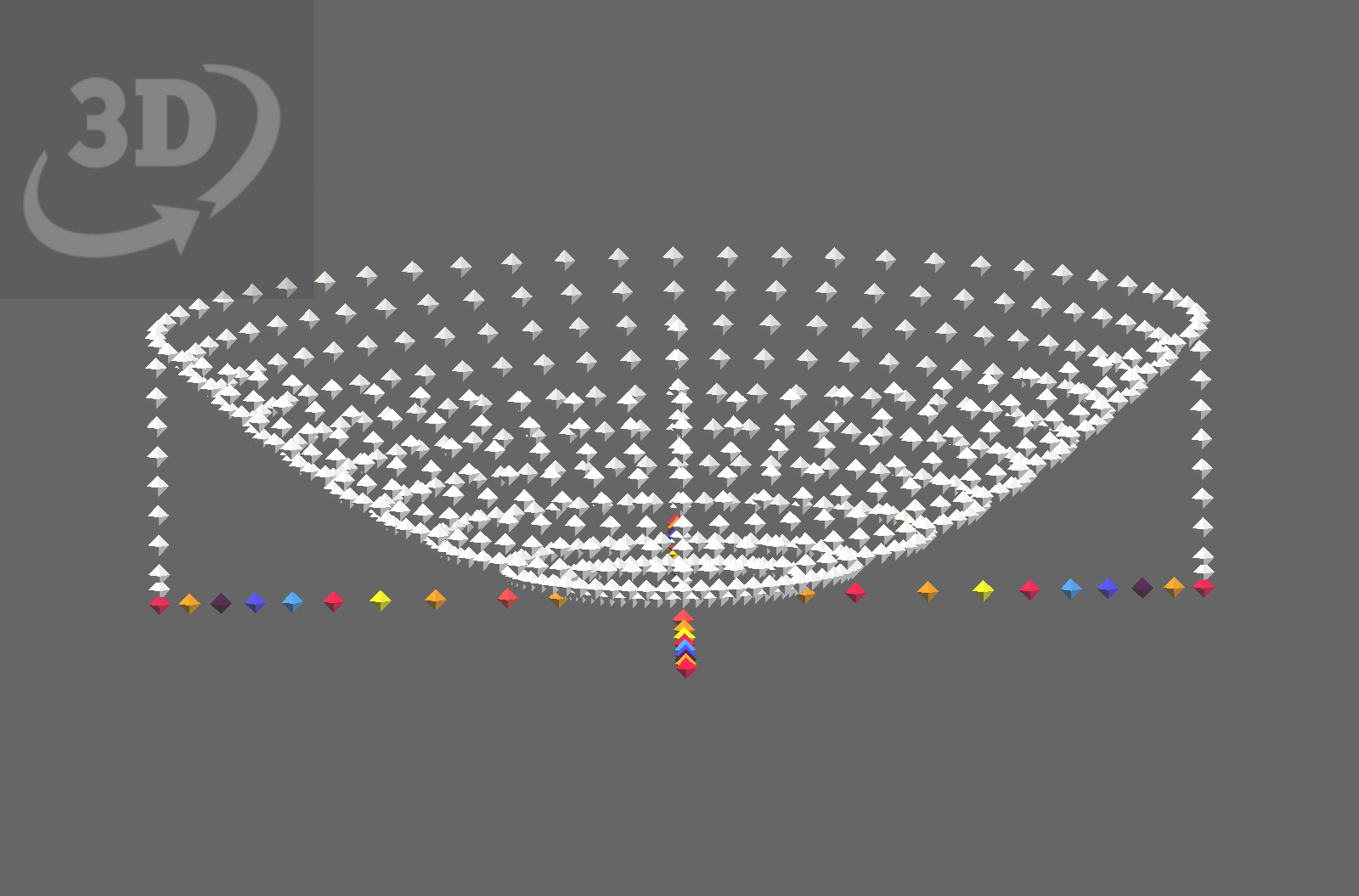
These are some models of paraboloids. They are of both elliptical and hyperbolic form. Scenes shows a graphical construction of a parabola, indicated by grid points, which is copied 60-fold around a vertical axis.
A 3D design created in vZome. Use your mouse or touch to interact.
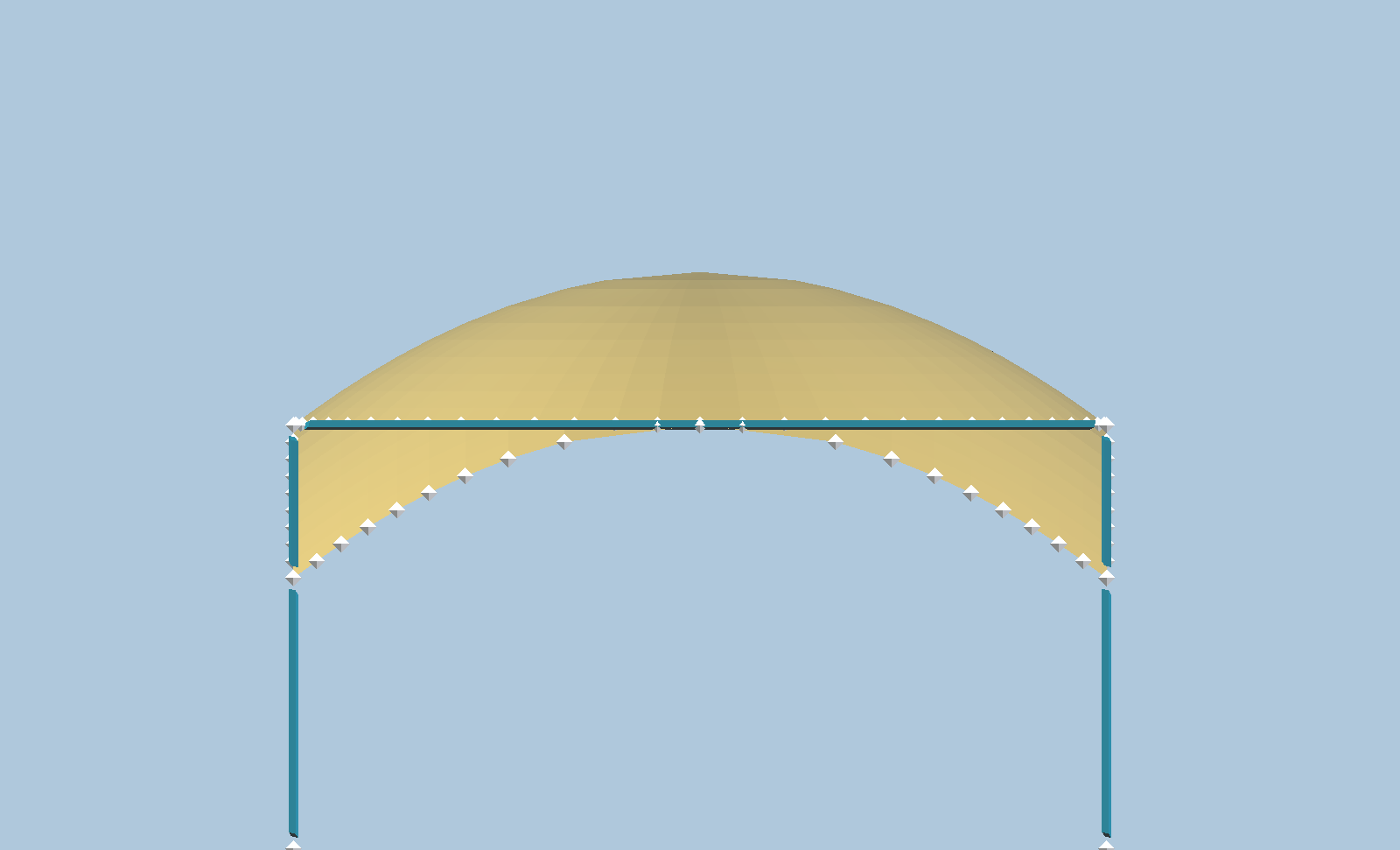
Below is a paraboloid intersecting a cube frame, with panels filled in.
The curving surfaces in these models are indicated by points and reference lines. The parabola shown in Scenes is generated graphically using √n values for points along x axis, and integer or rational values on vertical axis. Below, parabolas are used to compose a hyperbolic paraboloid, known as a Hypar, indicated by points, as with the circular one above. Scenes shows section planes and a sample of double ruling, where the surface has two straight lines on it intersecting at each point on it.

Below is a model of a framing system using the √n series system shown for layout of parabolas. In this model, it is an elliptical paraboloid, rather than the circular one shown above, which is a special case. This model shows how a standard framing member can be cut to the parabola layout line, and recombined as a curved member. Paraboloids have a property which facilitates buiding, which is that all sections parallel with coordinate planes are the same, so one template works for all in xz plane, and one for all in yz plane. Scenes shows an elliptical section plane.

Below is another application of paraboloid surfaces in a building context. Sections of circular paraboloids are reoriented and combined as petal shaped quadrants of a roof.


Another roof structure can be viewed Here
An elliptical paraboloid bowl