These models illustrate stacking of spheres, represented by polyhedra. These balls are not featureless spheres, but have vertices equidistant from their centers, which serve as bonding sites, symmetrically distributed so that balls in an array can share points. This makes for a good visual representation of tangent spheres, arranged in stacking patterns. These patterns are well documented and explained in articles such as this .
What is offered here is 3D interactive modeling, and a focus on geometric descriptions of the different stacking arrays.
In Scenes, the first 3 models show a ball that is inscibed in a cube, in contact at the centers of its faces, and arrays that result from parallel balls attached to the original one at these tangent points.
The next 3 models show a ball that is enlarged relative to a cube, so that it makes contact with the cube at the centers of its edges, which can be seen to be the centers of faces of a Rhombic Dodecahedron. The arrays that result from attaching parallel balls at these points are shown.
The last 4 models show a ball that is further enlarged relative to a cube, so that it coincides with the cube at its corners, which are at the centers of the hexagonal faces of a Truncated Octahedron. The arrays that result from attaching parallel balls at these points are shown, including a sample of diamond lattice.
All 3 of the polyhedra shown as framwworks with balls inscribed, the Cube, the Rhonbic Dodecahedron, and the Truncated Octahedron, are units that fill space with no gaps between.
A 3D design created in vZome. Use your mouse or touch to interact.
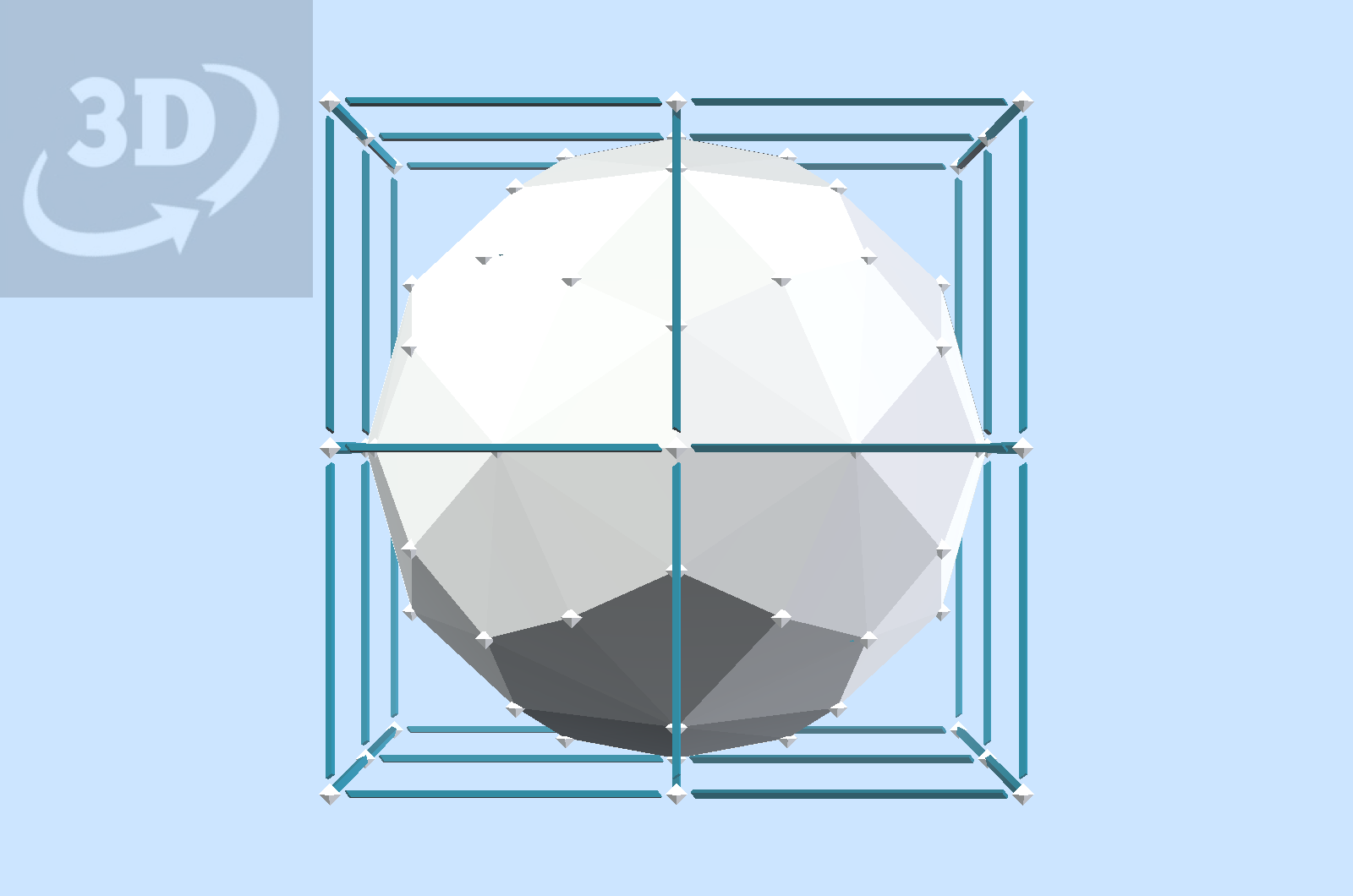
Here is shown another kind of stacking of spheres represented by polyhedral balls. A ball is inscibed in a Pentagonal Dodecahedron, intersecting its edge centers. Parallel balls can be attached at these points, resulting in an array of 12 balls in icosahedral symmetry. This arrangement can be seen to surround a similar ball, which must be scaled down to fit tangent to all of the 12. This kind of array can be extended in various ways concentrically, but not as a uniform lattice.
