Close packing of spheres represented by polyhedra. While many polyhedra have some or all of their vertices on an indicated spherical surface, only some have vertices in requisite positions to compose arrays that represent close packing. The first example is this, which vZome users will recognise as Octahedral Symmetry Trackball. It has a set of vertices that allow building the FCC pattern. However, it does not have all the vertices needed to compose HCP packing.
A 3D design created in vZome. Use your mouse or touch to interact.

Here, Cuboctahedra are sharing vertices to compose an FCC array. These also lack the vertices for HCP.

Anticuboctahedra can be used to build HCP arrays, but not FCC.
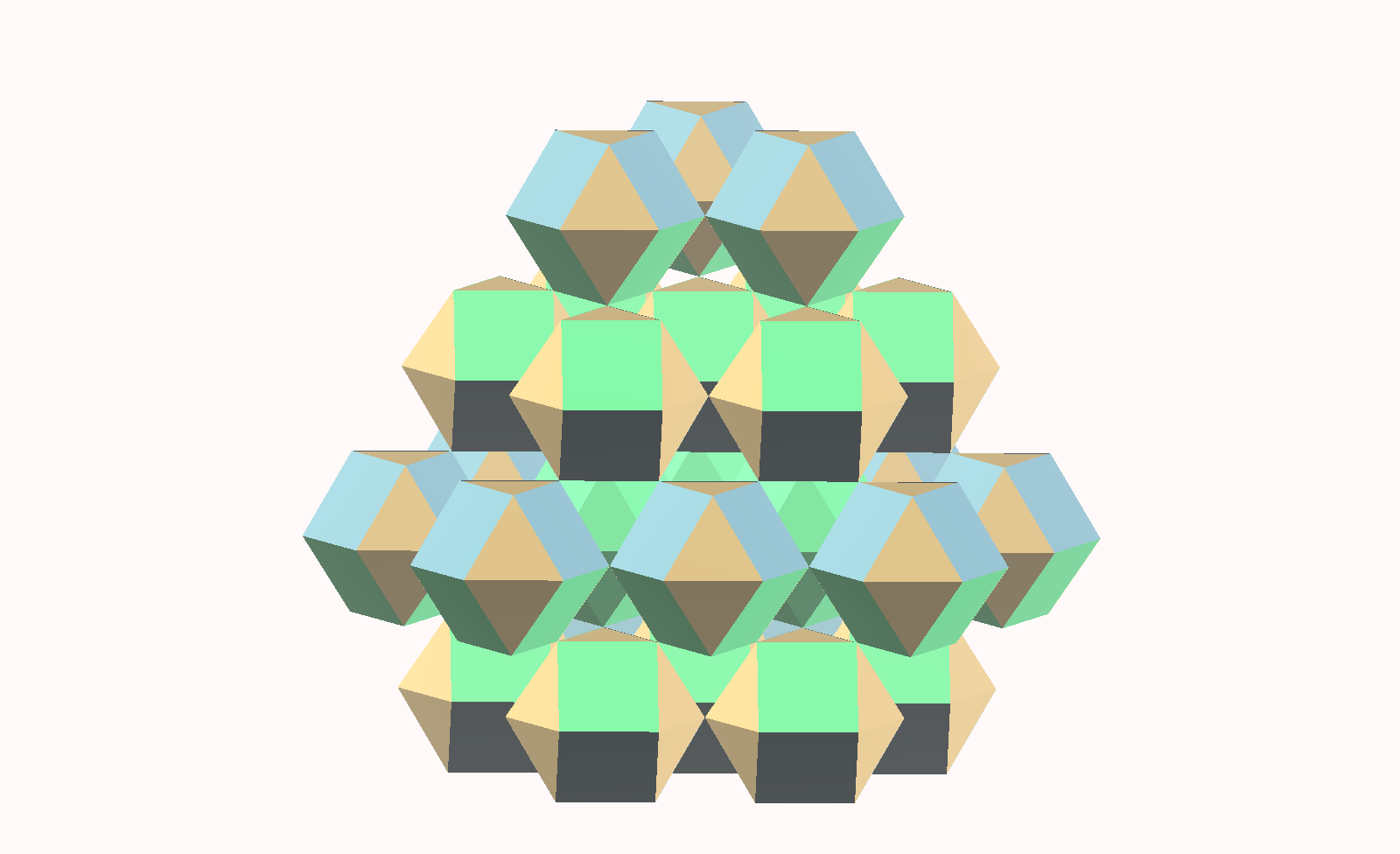
A study of this Polar Triacontahedron reveals that some of the vertices as well as the centers of some of the faces are all equidistant from the origin, and are in the right positions to represent spheres in close packing arrays.

We can add chords between these selected points, and build this type of Ortho Birotunda, which has all the points needed. It has the vertices of both Cuboctahedra and Anticuboctahedra.

These polyhedra can compose FCC arrays. Polar caps are added as open frames, just to enhance the spherical forms.

They also serve for HCP arrays.
