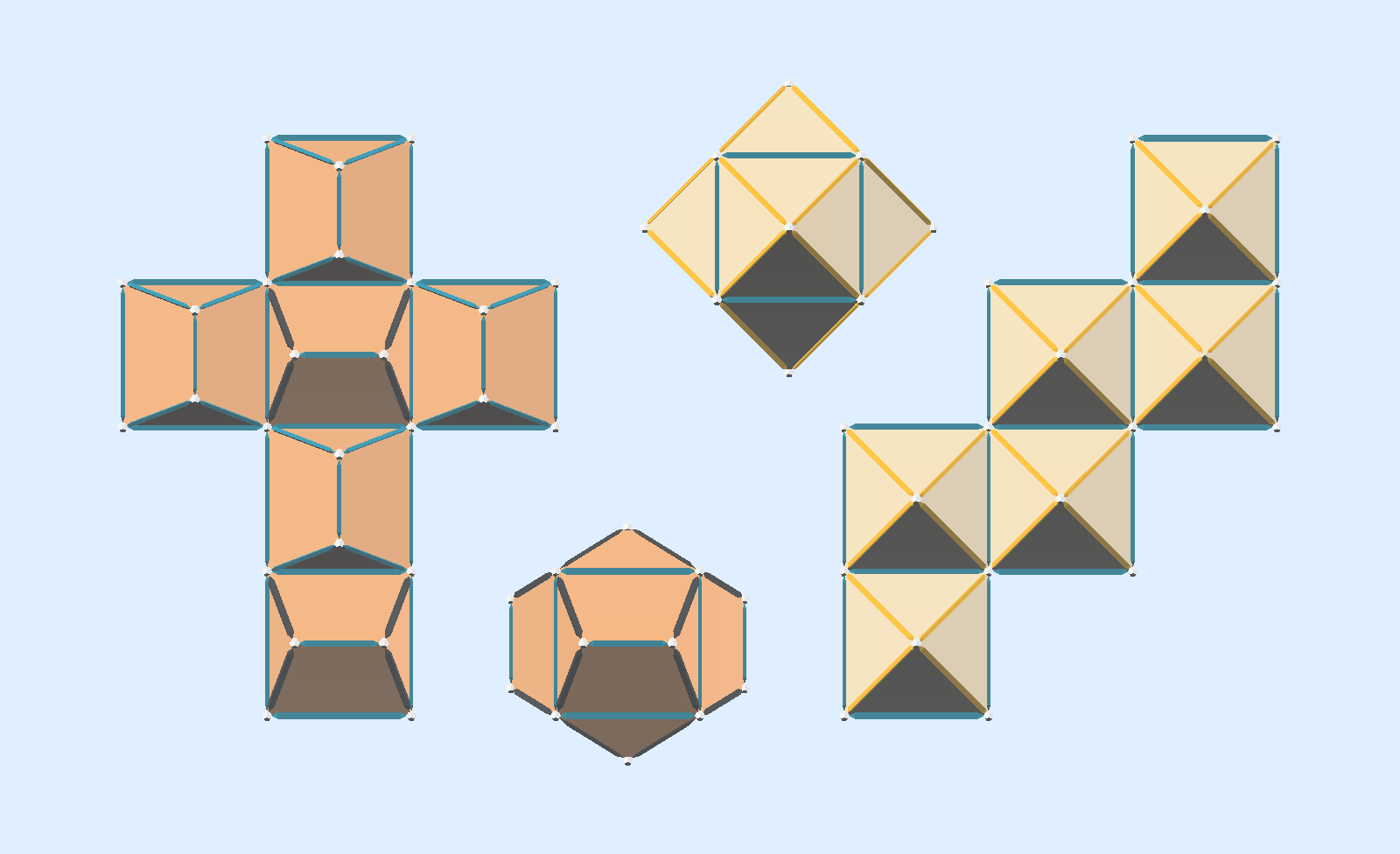
An array of regular pentagonal Dodecahedra in Icosahedral symmetry. Twelve units surround an Icosidodecahedron, sharing edges with adjacent units. There are unfilled spaces between dodecahedra.
A 3D design created in vZome. Use your mouse or touch to interact.
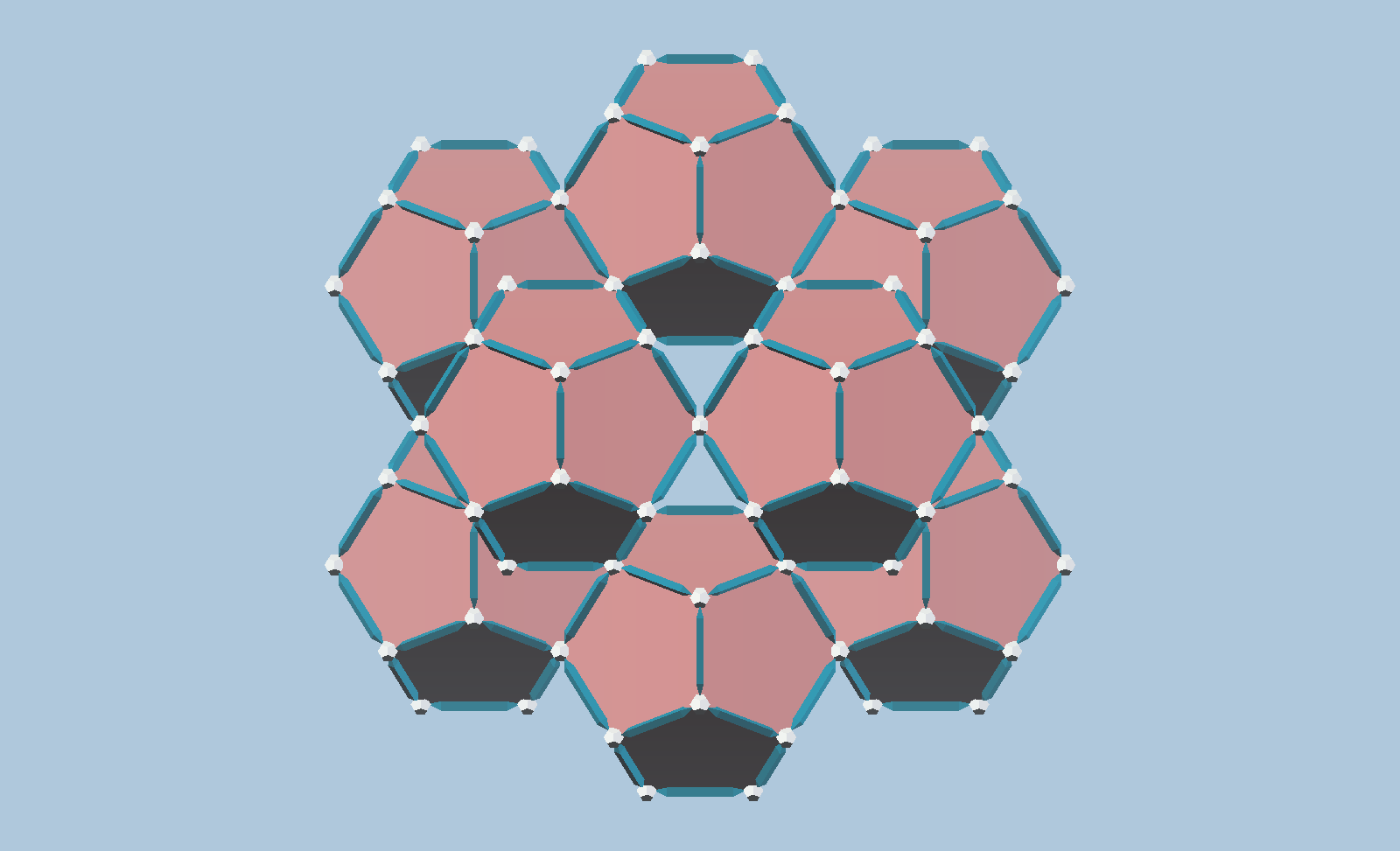
Further out from the center, a larger Icosahedral symmetry array can be built, likewise with Dodecahedra sharing edges with neighbors, and also having unfilled spaces between units. Larger concentric “shells” of dodecahedra can be composed in similar fashion. These are by no means the only ways to arrange dodecahedra in icosahedral symmetry, just relatively simple configurations.

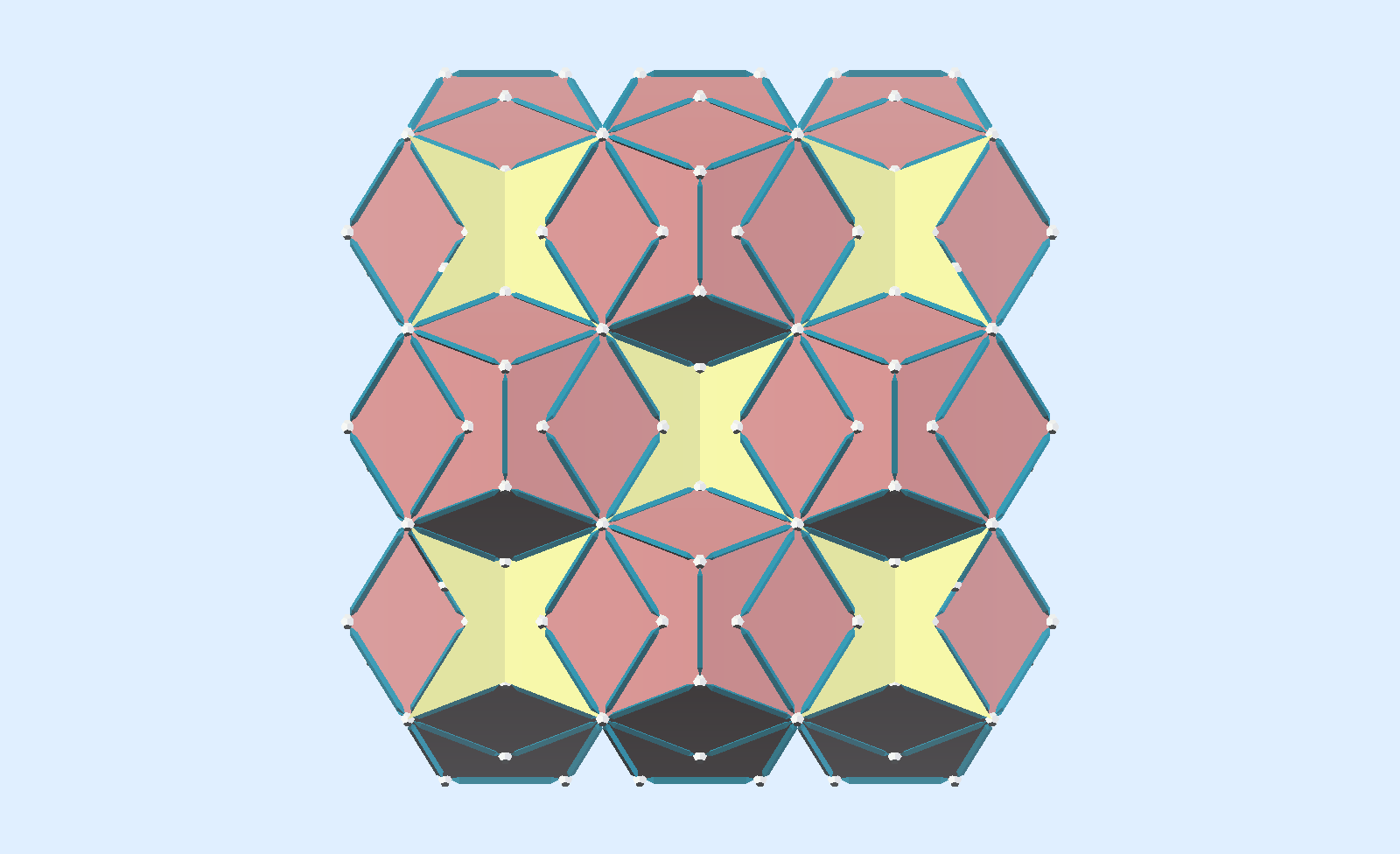
Another composition of arrays of Dodecahedra is this, with faces of units coplanar with faces of neighbors. Faces do not fully coincide, but have rhombi as the shared part of both pentagons. The dodecahedra are thus shifted, and the array is in Octahedral symmetry. In this arrangement, the Dodecahedra are stacked more compactly, and all the spaces between them are filled with one kind of concave dodecahedron. The framewok of this is Zometool buildable.
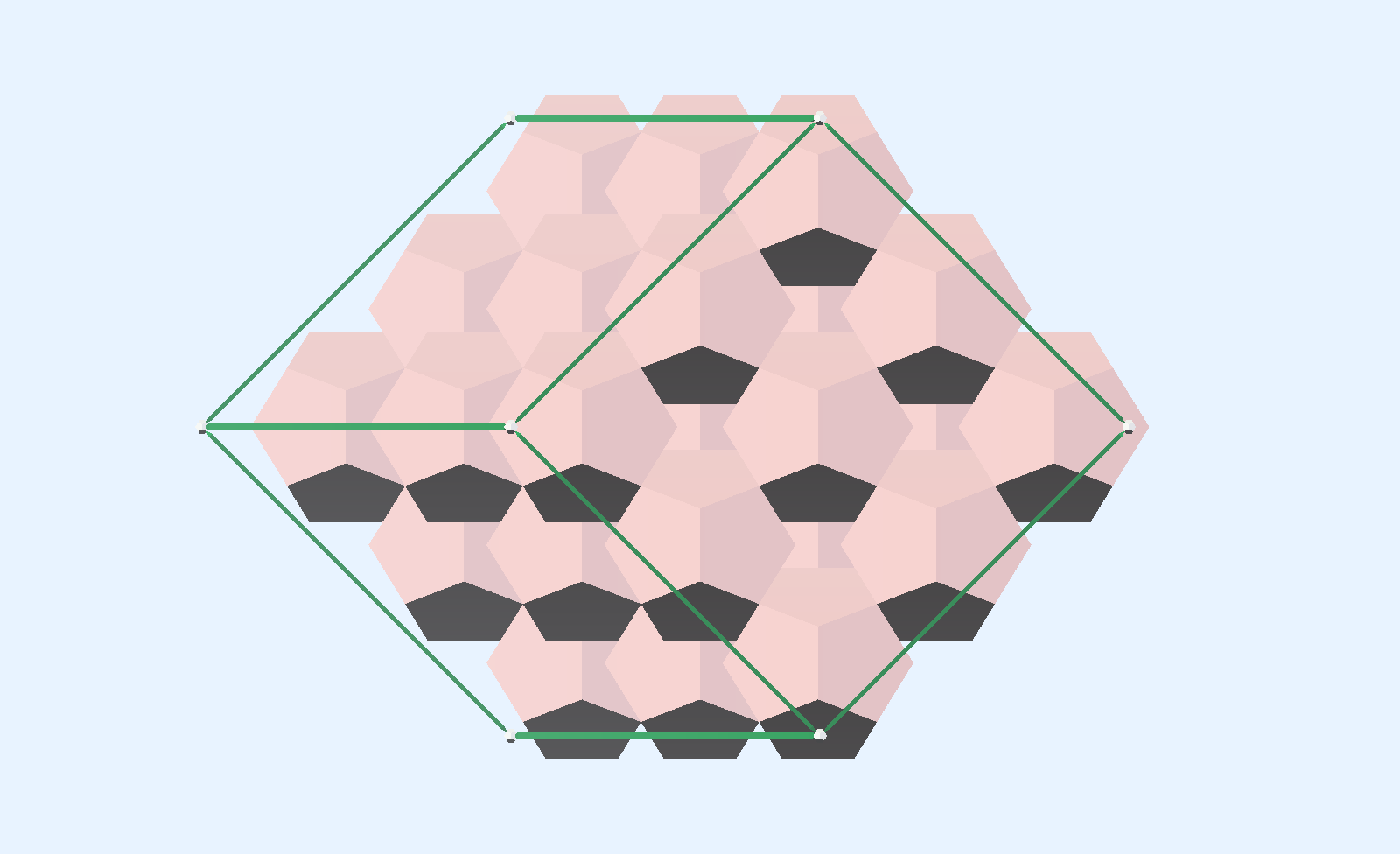
An extended array, with exterior green lines, showing how the rows of Dodecahedra are aligned with Oct-Tet directions.
This shows how 6 concave dodecahedra surrounding a convex one fit between 6 convex ones, in the positions they are in as part of an Octahedral array.
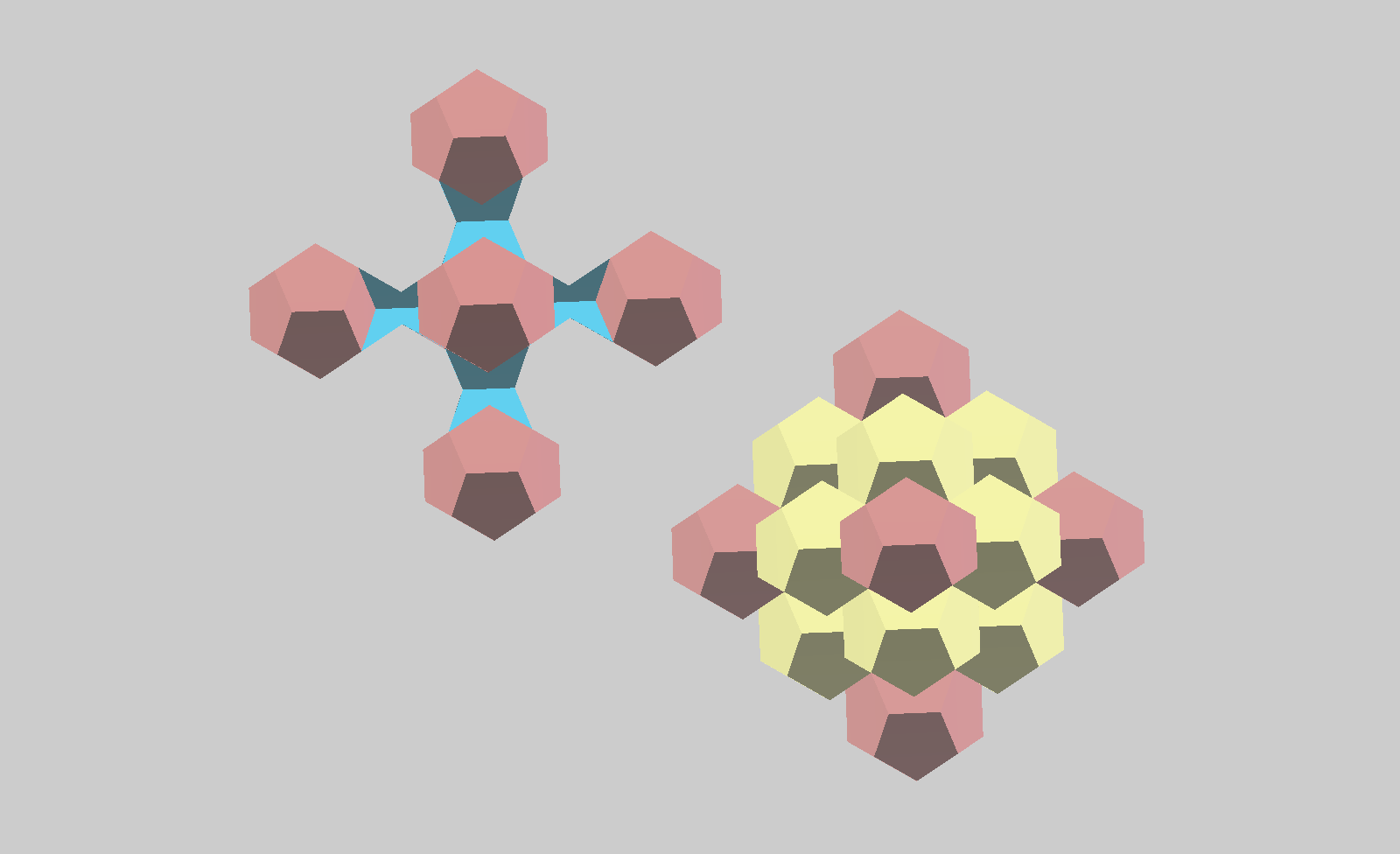
Another kind of array is this, where the Pentagonal Dodecahedra have a Cubic grid in common with Rhombic Dodecahedra, and the two systems partially overlap. Both kinds of dodecahedra are truncated into 6 blocks around a cube, which are placed sharing a common square face, paired with one of the other type. One paired block of each type is shown pulled out from its position in the grid, revealing how the blocks fit together. Note that there are concave dodecahedral spaces in the centers of the cubes where 6 of the blocks cut from pentagonal dodecahedra converge.
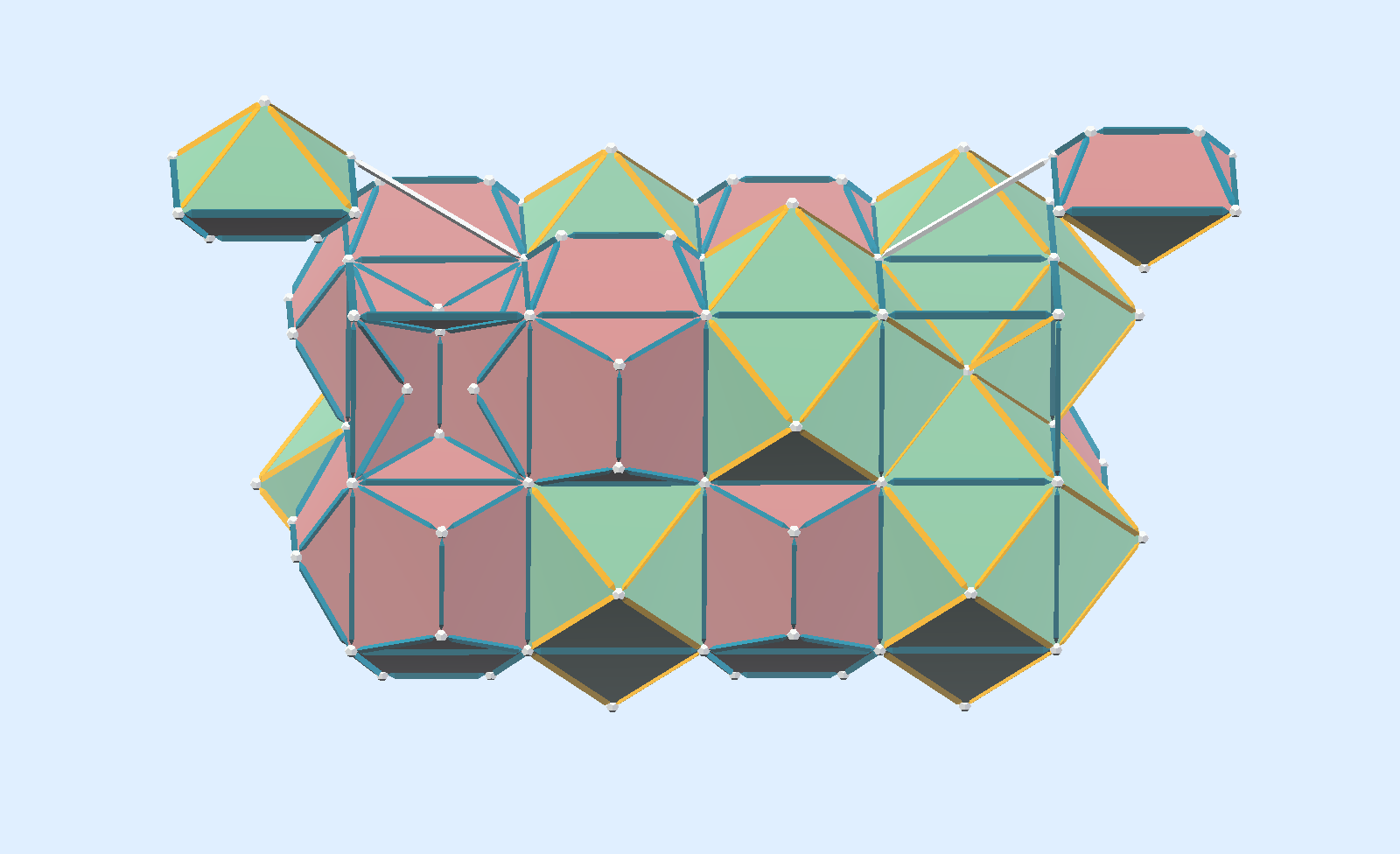
This shows two kinds of “nets” which, if constructed with some hinging system, allows the whole configuration to fold into one or the other of the two kinds of Dodecahedron, as shown. This displays a kind of inversion. This has been done successfully with cubenets of 6 squares each made of some durable material such as Tyvek, sandwiched in between the blocks to serve as hinges. It is also possible to make the pairs of blocks with magnets imbedded so the whole assembly can be taken apart and inverted, one paired block at a time. Having multiple sets of blocks like this allows building larger arrays. We call sets of 6 of these paired blocks a Double Dodecahedron.