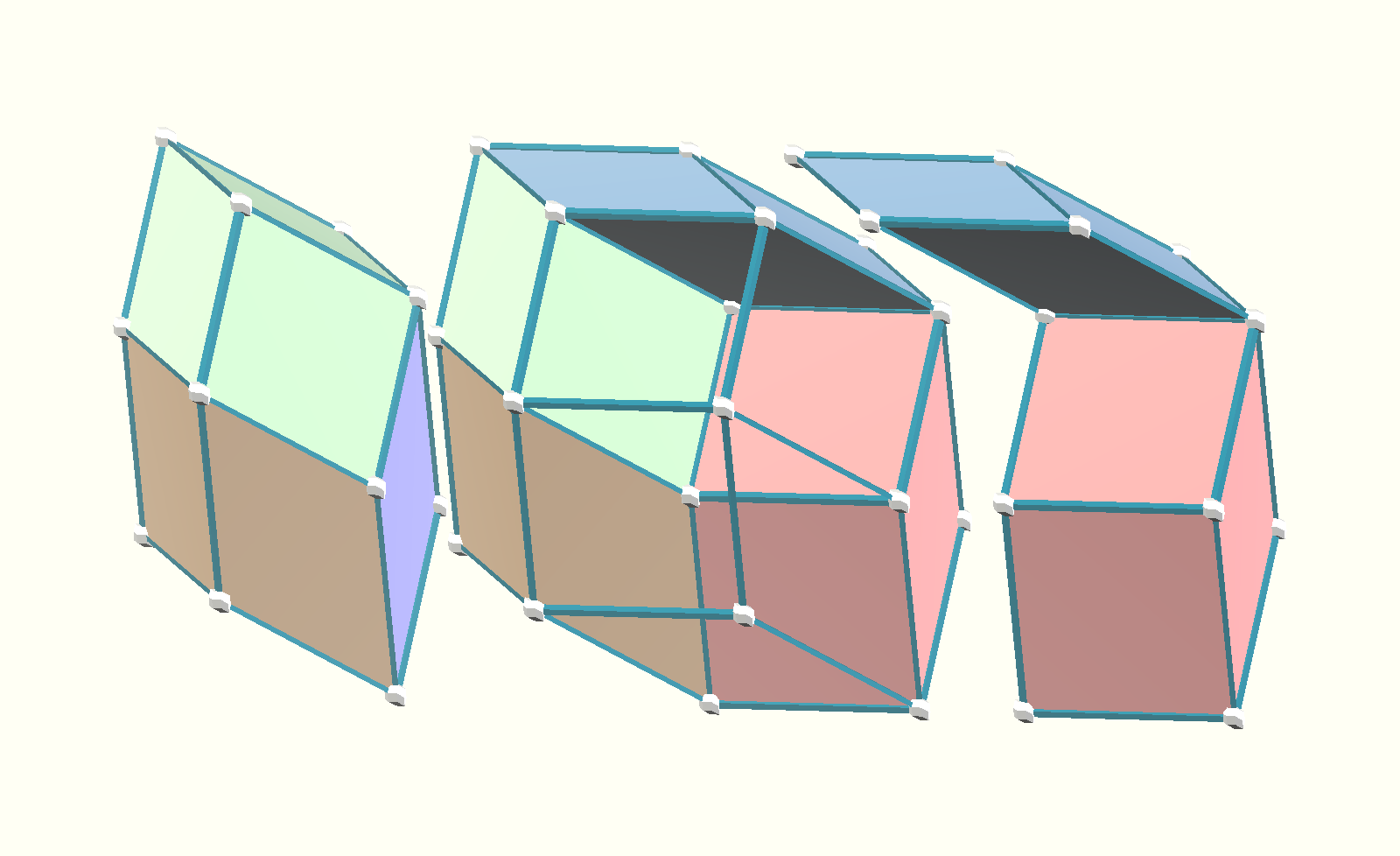
Showing dissection of a Rhombic Icosahedron. To the right are two types of hexahedron, a prolate, wedge shape, and an oblate, lozenge shape. To the left is an eccentric rhombic dodecahedron, which is composed of two of each type of hexahedron. A Rhombic Icosahedron can be dissected into five of each type. There is a canonical RI, which has all golden rhombus faces, and there can be any number of other variants with 2 types of rhombic faces. This pattern of dissection applies to all. Several of the variants of RI that can be constructed with vZome are incorporated in this, another model, as a Sequence
This page relates to Filling Space With Six Directional Polar Zonohedra
A 3D design created in vZome. Use your mouse or touch to interact.
This shows five directions as lines from vertices through the center of a pentagonal antiprism. In this form, the height of the antiprism is set so that non-adjacent radial lines are at right angles. In this angular arrangement, adjacent radial lines meet at ArcCos 1/𝜑 = 51.827…° This is built in √𝜑 field.

Using the five directions of struts defined this way as a coordinate system, a Rhombic Icosahedron can be constructed from a polar vertex, where all five intersect. An interesting feature of this variant of RI, which can be called normalized, is that the face angles also appear as dihedral angles. Two Rhombic Icosas can be connected at a shared polar vertex, and ten of the wedge type of hexahedra can share the same vertex. This array is constructed in this way, with 5 RI cells nested in, each sharing a face with one of the central RIs, and with two hexahedra, and sharing edges with each other as they as they compose a ring. From this arrangement, there are a couple of ways to build out with selected polyhedra drawn from the dissection of the RI. Generally, RI cells can be packed in various ways around the central polar axis, with the spaces between them fillable with subcells all of which have all of their edges parallel with one of the five coordinate directions. Thus these arrays are zonal.

RI cells can be connected at polar vertices, like strings of beads. Connecting the ring of five in this way leaves spaces that can be filled with dodecahedral cells, and hexahedral cells betrween. This kind of packing can be carried out further around the axis in an Extended Array. This array is directional along the polar axis, there is an “Up” and “Down”, showing here as an umbrella form. It can be periodic along the polar axis
Another way to build out is to nest another five RI cells around the axis in alternate positions, that do not connect end to end with the first ring of five. Carrying this pattern out further can build an array that is dipolar, rather than directional. Here, the ‘Up” and “Down” are equivalent, though not reflectively symmetric. Both of these arrays can have fivefold rotational symmetry about the axis, and have five planes of reflective symmetry intersecting the axis.

One extended array of this dipolar type looks like This.
Another extended dipolar array. In this model, one can see that RI cells in the outer course connect end to end, but only in pairs.

Another view of an array of the directional type is this. Note that all rhombic faces are left open. This gives views of the cellular packing, and also illustrates that this kind of array can be constructed using only squares joined edge to edge.

This is an example of a directional type of array, which has a slightly different set of five directions. Here, rather than the “normalized” directions, the edges are all parallel with a set of what we know as green struts in Zometool/vZome. These are Oct-Tet directions, and the selection is from how they occur as chords in a dodecahedron, one from each of five interlinked tetrahedra.
Another way to build out from two RI cells sharing a polar vertex is to fill in from the common origin with ten of the oblate type of hexahedra. This is a chiral array, with five-fold rotational symmetry about the axis, but no reflection planes.

Filling in some of the spiralling grooves, it is apparent that this pattern builds a double length RI. This is a kind of self-similarity, which can be carried out recursively.

This page is not intended as a proof of space filling patterns, just a demonstration of what appears to meet the definition.