A study of polar zonohedra with six directions, with a focus on space filling arrays.
This is related to Filling Space in a five directional System
A 3D design created in vZome. Use your mouse or touch to interact.
There are two types of six directional polar zonohedra in this study. The first type has six-fold symmetry about the polar axis.
This model shows a basic array of two of this type of Polar Triacontahedron sharing a polar vertex, with six dodecahedral cells also sharing the same origin point.

This shows Dissections of this type of Polar Triacon.
Note that the array model above uses only two types of polyhedra drawn from this dissection, in addition to the Polar Triacons. These are dodecahedra and cubes. Cubes are in two orientations, rotated about their respective three-fold axes 60° from each other, about the polar axis.
Faces in this set of polyhedra are squares, ArcCos 1/3 = 70.528…°rhombi and Arccos 2/3 = 48.1896..° rhombi.
This is a model of an extended array, in which can be seen how this packing can have full hexagonal symmetry about the polar axis, and also how the array can be periodic along the axis.

Below is a second type of packing of Polar Triacons, where the central axis is surrounded by a ring of six major cells, connected at shared vertices, rather than faces. This arrangement uses a second type of rhombic dodecahedra from the dissection, in addition to the cubes and dodecahedral cells used in the first type of packing. This pattern can also be extended.

This shows a pair of the second type of Polar Triacontahedron. This type also has two sets of cubic systems, but rotated around their respective three-fold axes only 44.48° from each other, which makes them aligned with two of the five orientations of cubic systems in icosahedral symmetry. One cube each of the two orientations are shown “drawn out” from their positions in the Polar Triacons. The faces in this set of polyhedra are squares, 72° rhombi, 60° rhombi, and 36° rhombi.
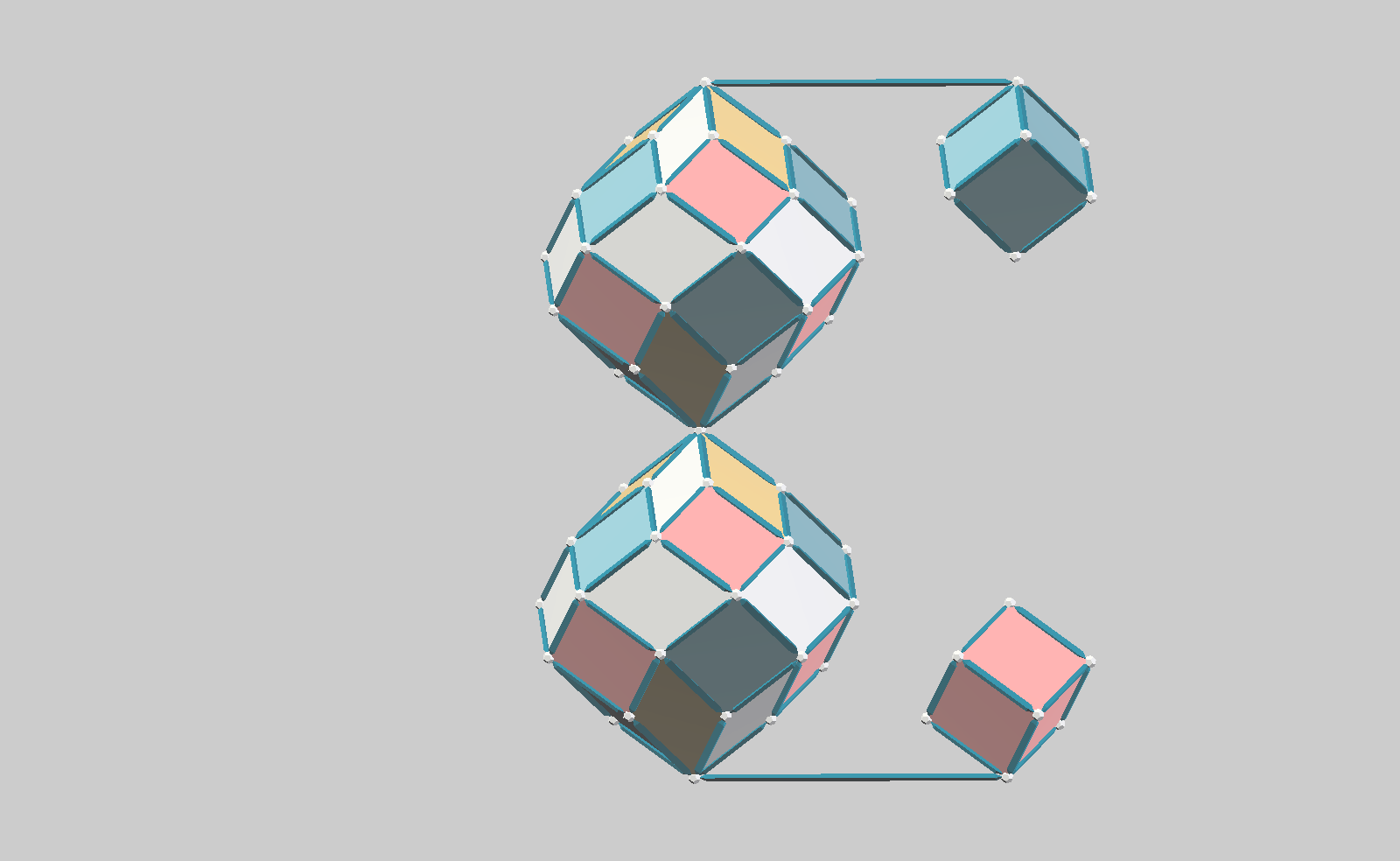
This is an extended array, which shows that while the array can be periodic along the polar axis, it can only have three-fold symmetry about the axis.

This shows a chiral arrangement, where two of the first type of Polar Triacon have oblate hexahedra drawn from the dissection sharing the origin point. This pattern is partially filled out to show that it builds a double length Polar Triacon, which is to say, a kind of self-similarity, which process can be repeated recursively.

Here is shown an array of affine Polar Triacons, with their associated dodecahedra and hexahedra. For reference an affine hexagon is delineated in the center of the array, as it appears on opening.
