An array of polar zonohedra built with seven directions of edges. Primary cells are 42-hedra, with spaces between them filled with hexahedra and dodecahedra composed from unit lengths parallel with some of the original seven. The array maintains the seven-fold rotational symmetry of the single 42-hedron.
This is a continuation of the studies Filling Space in a five directional System
and Filling space with Six Directional Polar Zonohedra
A 3D design created in vZome. Use your mouse or touch to interact.

Here, a 42-hedron is shown dissected into hexahedra. Thse hexahedra are of 4 types, each of which corresponds directly with a triangular section plane with the polar axis normal to it. Given that a regular heptagon of edge lenth e has two chord lengths, sigma (σ) and rho (ρ), the 4 types of triangles corresponding to hexahedra are: e-σ-e, e-σ-ρ, ρ-e-ρ, and σ-ρ-σ. Section planes show the full vatiety of triangles in this dissection, as they intersect hexahedra.
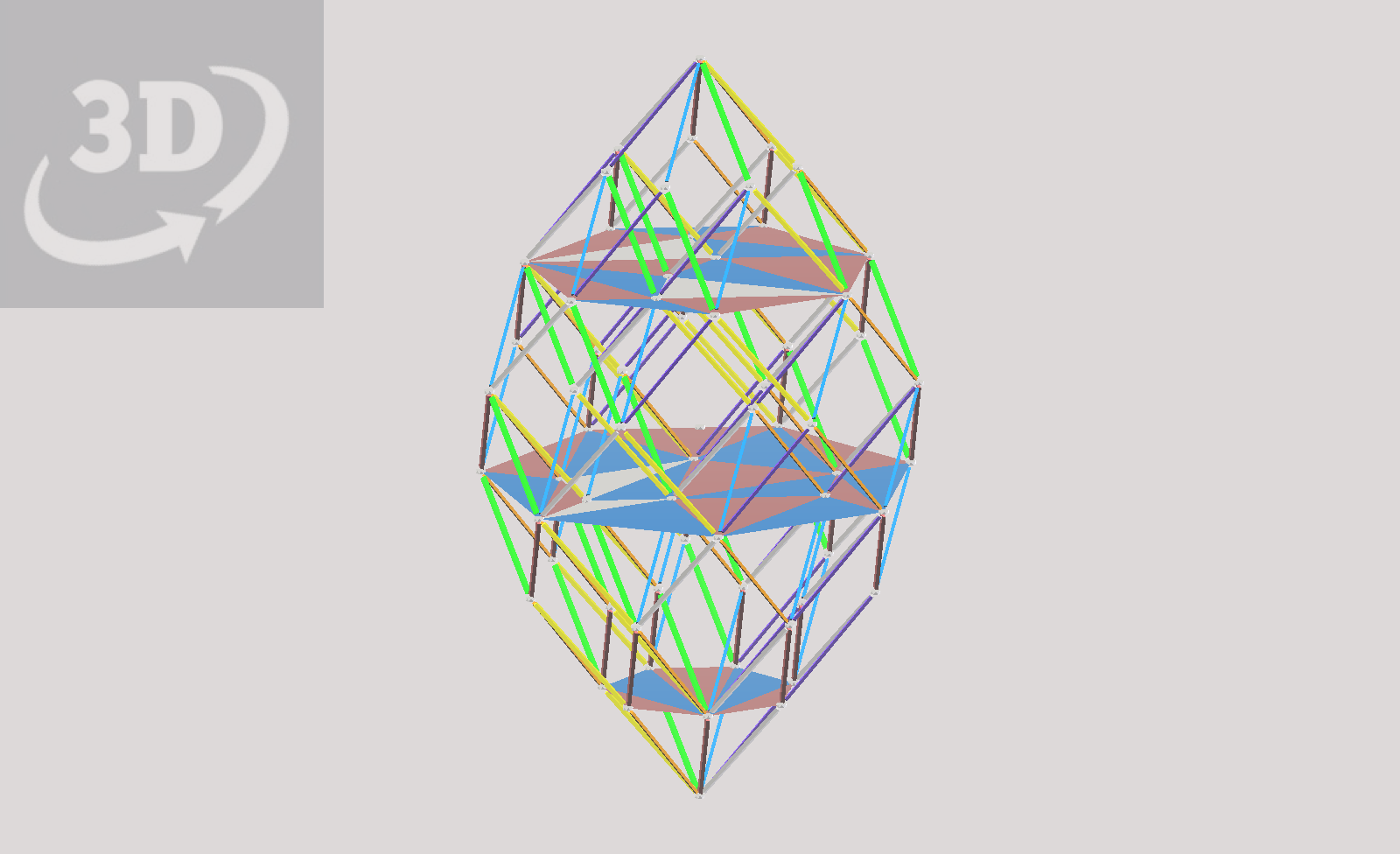
This is one form of extended array, building outward around the polar axis. Symmetry is maintained, including seven planes of reflective symmetry that pass through the axis. Note that this array, like the first one, has a directional character; It has “upward” and “downward” direction in relation to the polar axis, like an arrow, or a bowl.

This shows a dipolar array, where two arrays, of opposite direction, coincide at the origin. Thus there is an “equatorial” plane defined, with the “above” and “below” arrays being equivalent, though not mirrors of each other. This is a chiral composition, so has rotational symmetry, but no reflection planes.

This shows further extension of directional form of array. Thus far, patterns of composition can be found that are all zonohedra using only unit edge lengths drawn from the original seven. Some patterns lead to overlapping cells, which no longer meets the unit edge length requirement.

8 Direction Arrays is a continuation of this series of pages.