This is a study of interlinked polygons. There are several kinds of such “polylinks.” Here we are focused on those that define planes that intersect at a commmon origin point. This is a continuation of the subject material of 31 Great Circles In this first part, three and four plane models and expansions of them are featured.
The above model shows three rhombi interlinked. As in the model below, this illustrates a symmetry requirement for the perimeters of these figures to each be a continuous path that does not intersect the others.

Note that in the above model, the planar stars do not intersect each other. In the scenes dropdown menu, there is a view of 3 slightly elliptical dodecagons which interlink without intersecting each other This is intended to illustrate the weaving concept displayed in the following video, where the planes are composed of closed circles that are interwoven to form a symmetrical structure.
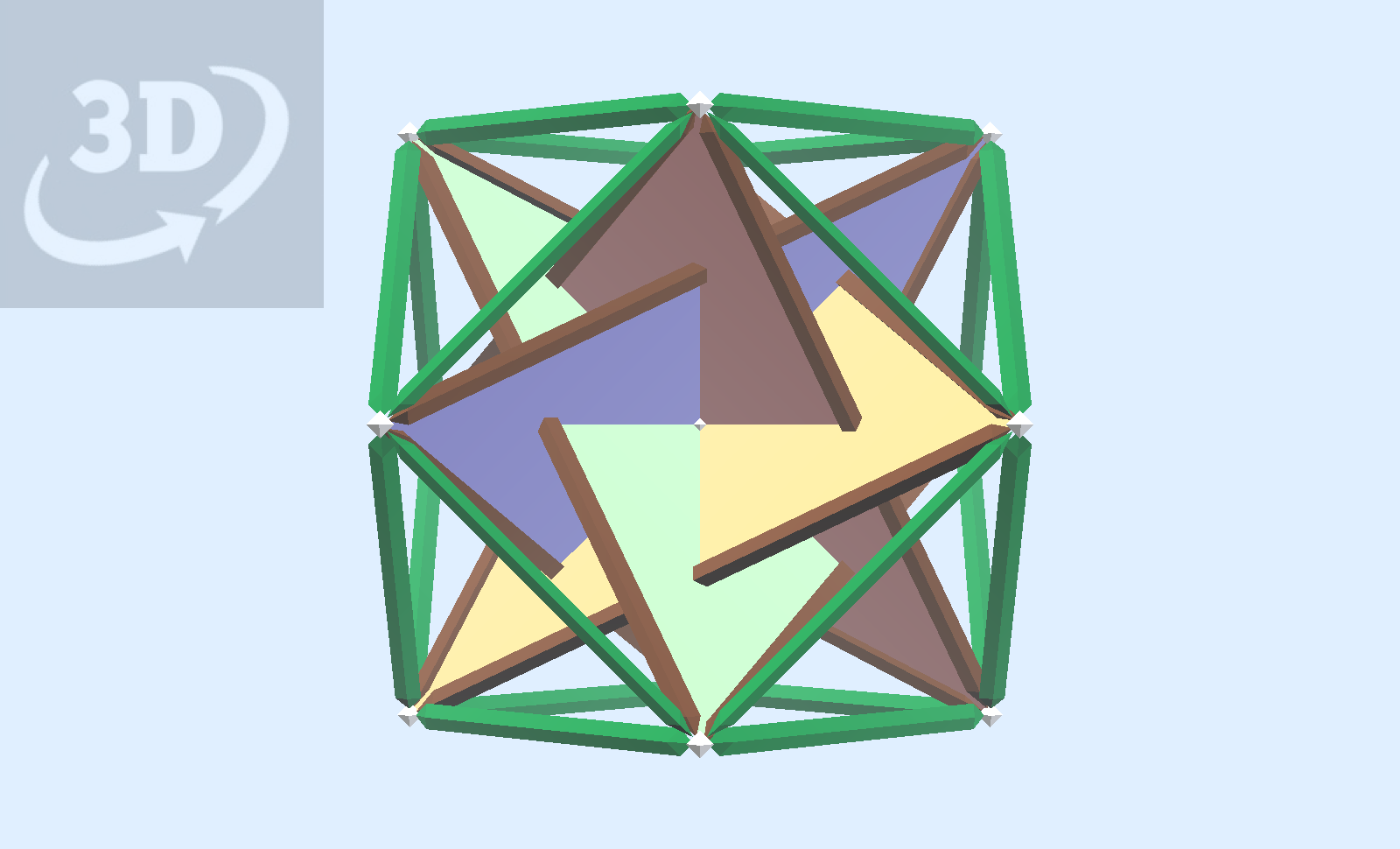
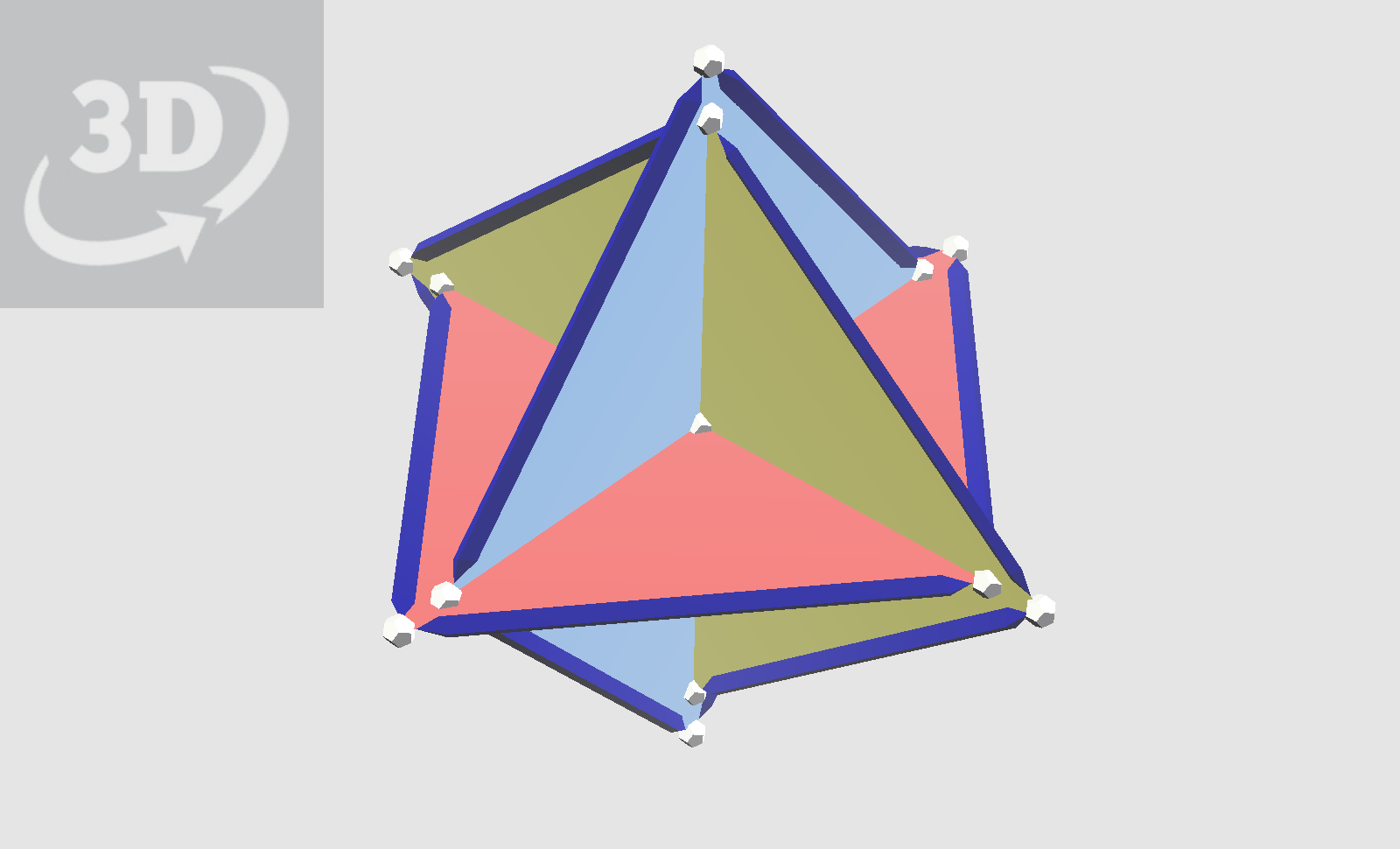
In the above model, the edges of equilateral triangles are chords of a Cuboctahedron. In the model below, these triangles are doubled with another set of four with alternate position, forming four hexagrams, also called a Cubocta Star
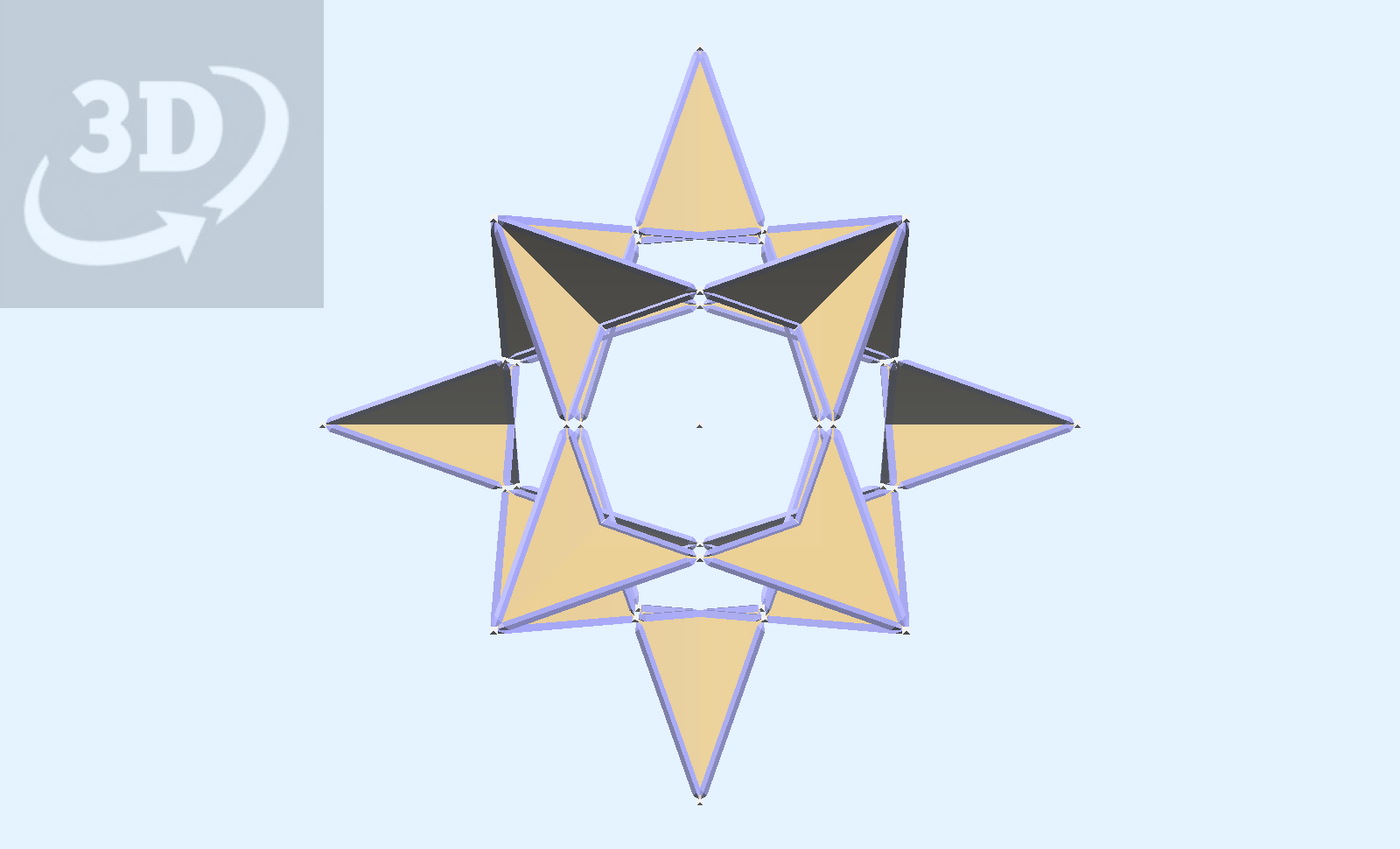
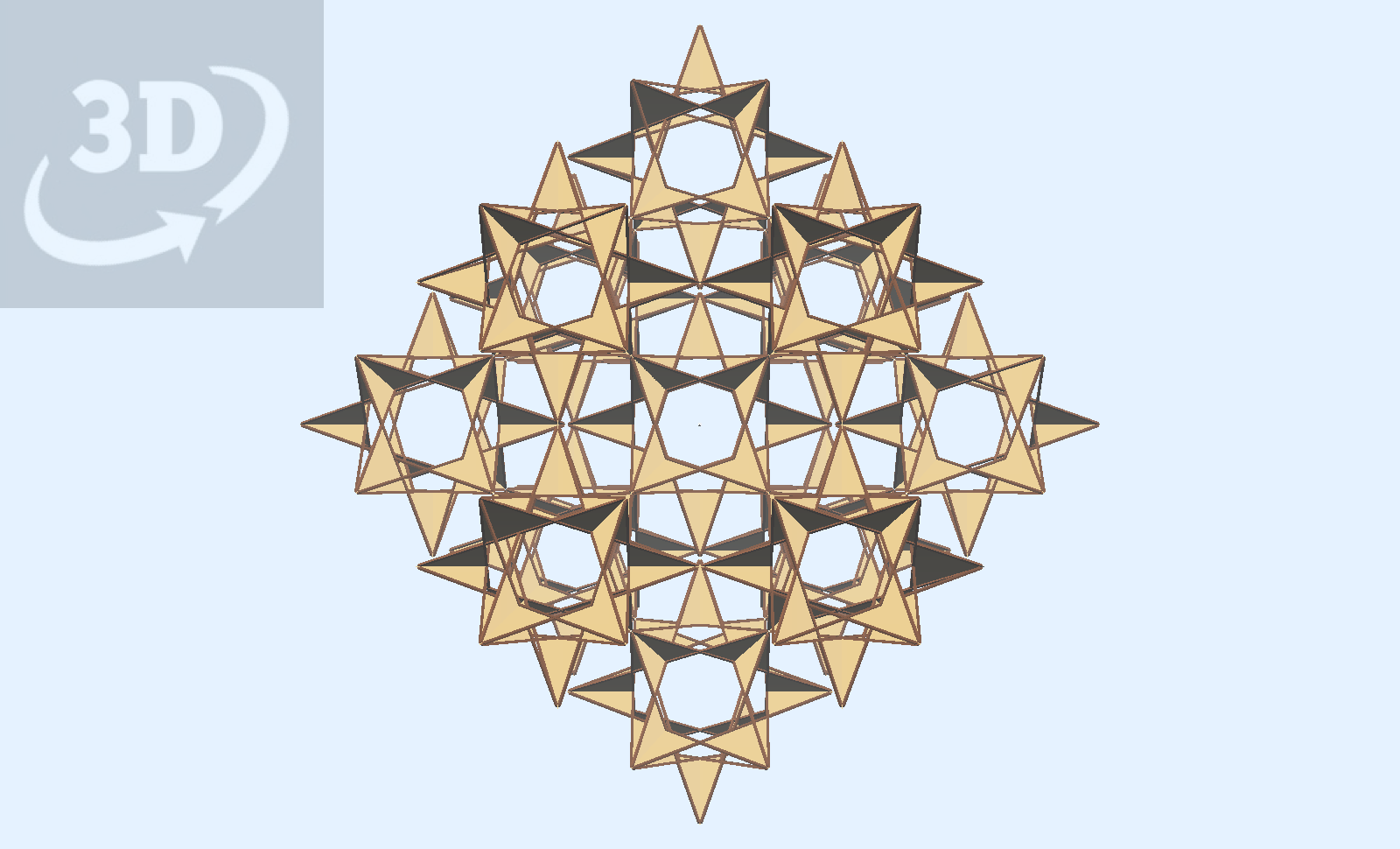
The above model shows the Cubocta Star in a periodic array.
Here is a Cubocta Star paneled. This design works very nicely as a porch light.

A continuation of this study can be seen Here