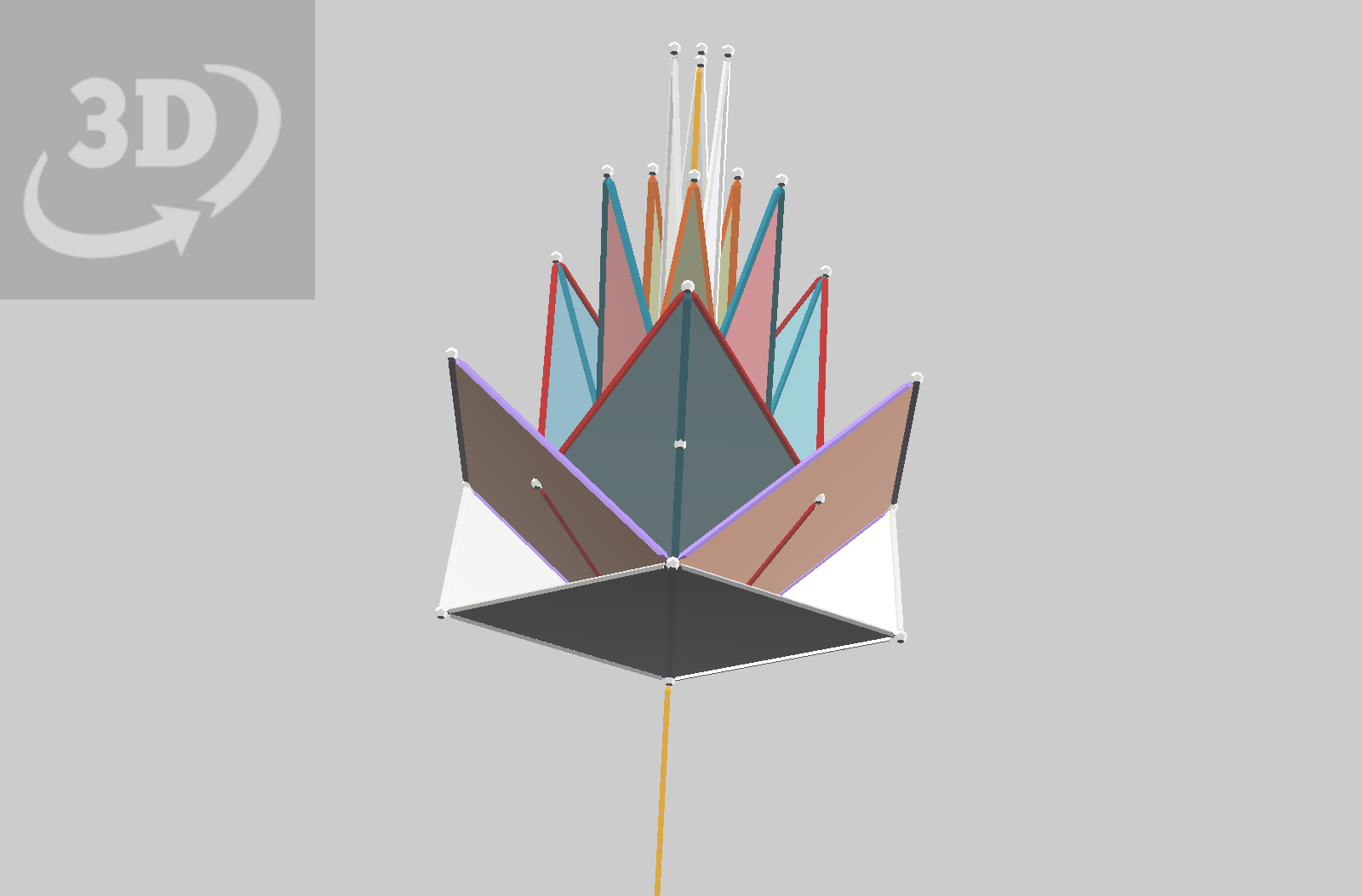
These are geometric figures that resemble flowers. A variety of Polar Zonohedra with shared origin points are used to compose these figures, Parts of these zonohedra are omitted. The first model below features five-fold symmetry about the polar axis. Scenes shows different compositions.
A 3D design created in vZome. Use your mouse or touch to interact.

Some years ago, I had the notion to make a Zometool model composed of parts of all the five-fold Polar Zonohedra that could be made, using the red, yellow blue and green struts. Arranging them about a common axis produces a form that has a resmblance to some flowers. When I began using vZome, I revisited this concept. With the ability to use more than one strut in pentagonal holes, and to panel, I made these models, still only using the strut colors/directions as in zometool. Composite flower and Chain of Rhombic Icosahedra
In the model above, I used a selection of other colors/directions that are availble with vZome. Building these figures is not intended to represent any particular flowers, just the form in a general way. Choices of which parts are combined are made more or less based on aesthetics, and conditions like not having the partial zonohedra overlap each other. All colors are default. In composing these models, there is a study of several kinds of symmetry and examples of each kind that can be found using the available directions. The model below, with it’s Scenes menu, features four-fold axial symmetry. The Polar Zonohedra of this kind are Rhombic Dodecahedra, which, as with the the Rhombic Icosahedra, range in proportioning, from squashed down, or oblate, to elongated, or prolate.

The models below are related, but feature examples that only have two-fold symmetry. This is less like actual flower forms, more about types of symmetry. In Scenes, there are also 2 examples of four-fold compositions that are constructed half from available directions and half from mirrored copies of directions. (Green plane mirrors) The one titled “Flower 3 4-fold by mirroring” is actually a kind of hybrid, as it has a 2-fold figure at the bottom.

Below is a model in three-fold symmetry, and others shown in Scenes. These are perhaps more evocative of more familiar flowers, such as tulips.