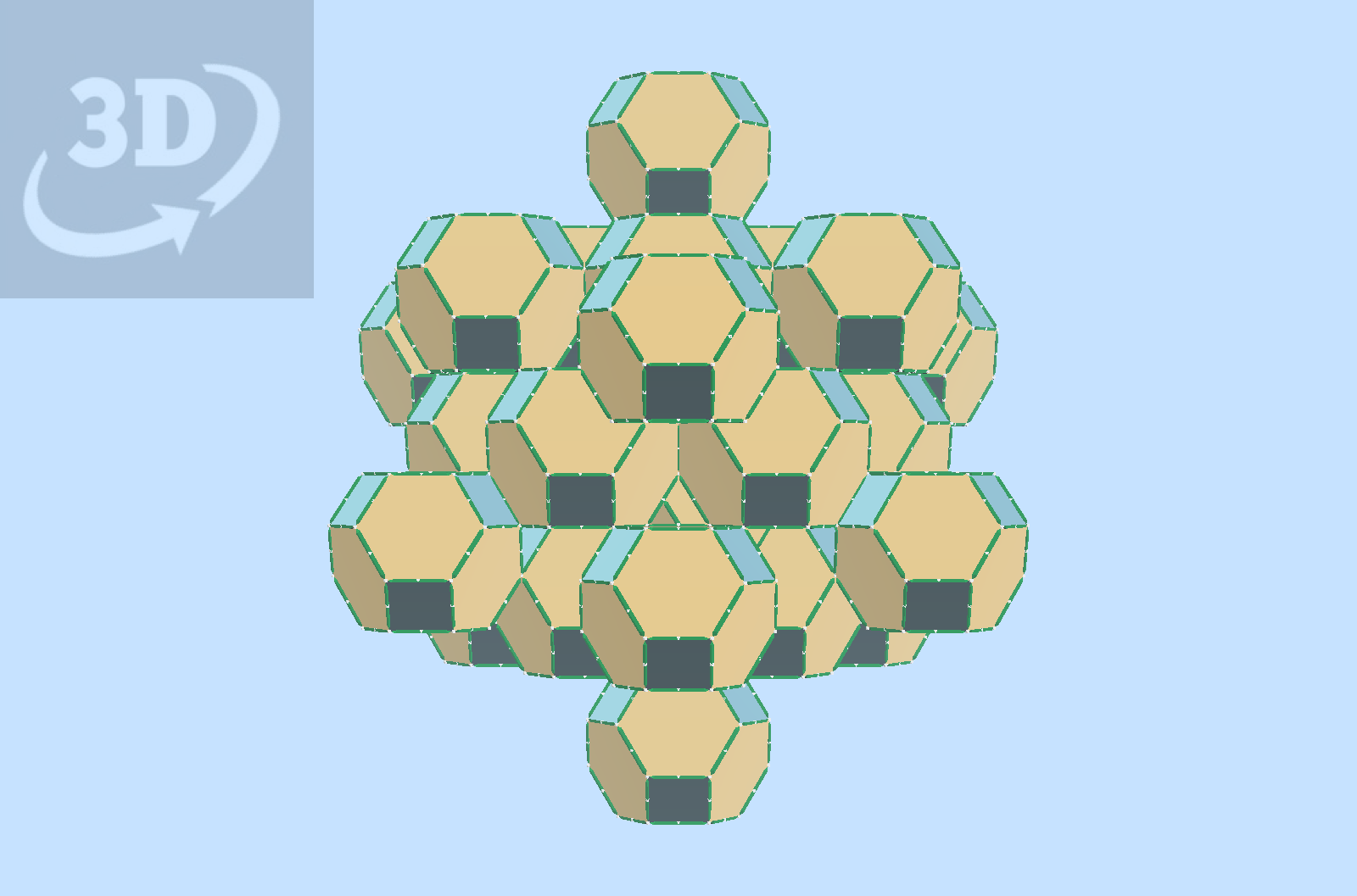
This exploration is a continuation of a study of polyhedra that can represent Close-packing of equal spheres Part 1 of this study can be seen Here
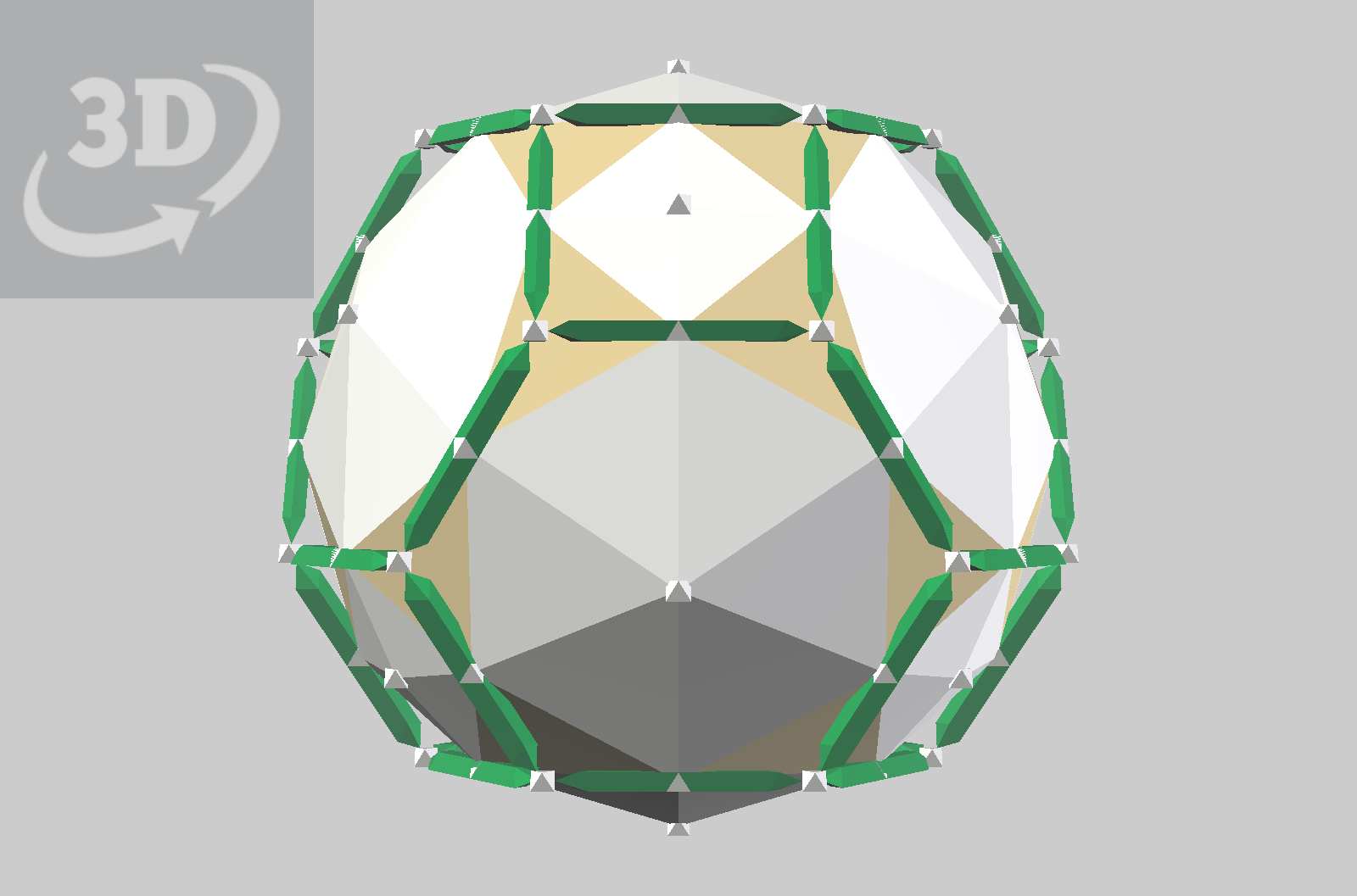
Here, a regular Truncated Octahedron has a polyhedron inscribed in it that can be seen as representing a sphere, as its’ vertices are all equidistant from the center, and the midpoints of the edges of the TO are all on the sphere surface, at positions that allow building close packed arrays, and other related patterns.
vZome users; Note that this 96-hedron has all the points indicating strut directions that appear on the √2 field trackball, with an additional set at the midpoints of edges of the TO that make squares.
A 3D design created in vZome. Use your mouse or touch to interact.
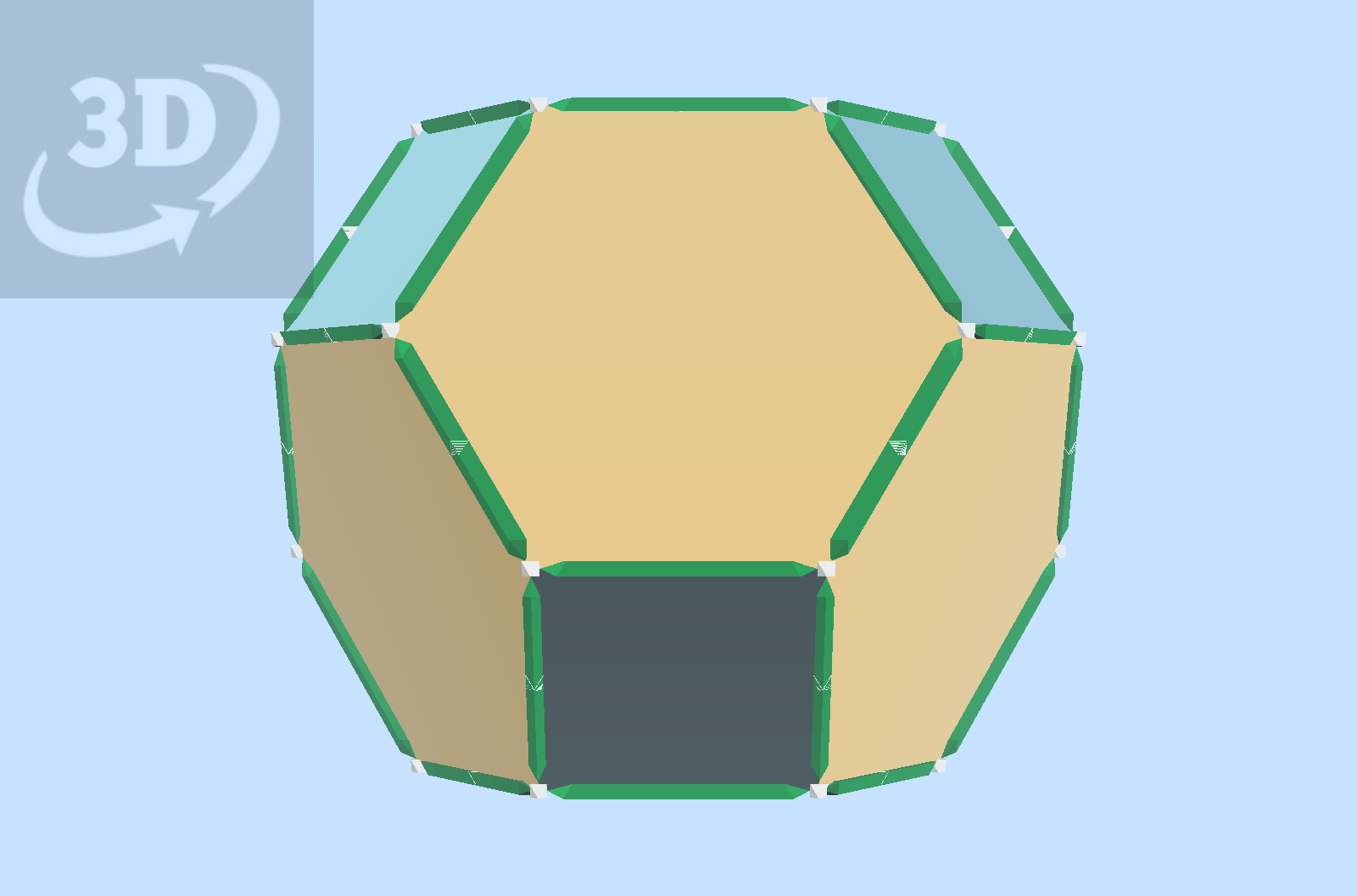
For simplicity of rendering, we can look at just the Truncated Octahedron that can have a sphere inscibed within it, and compose arrays.
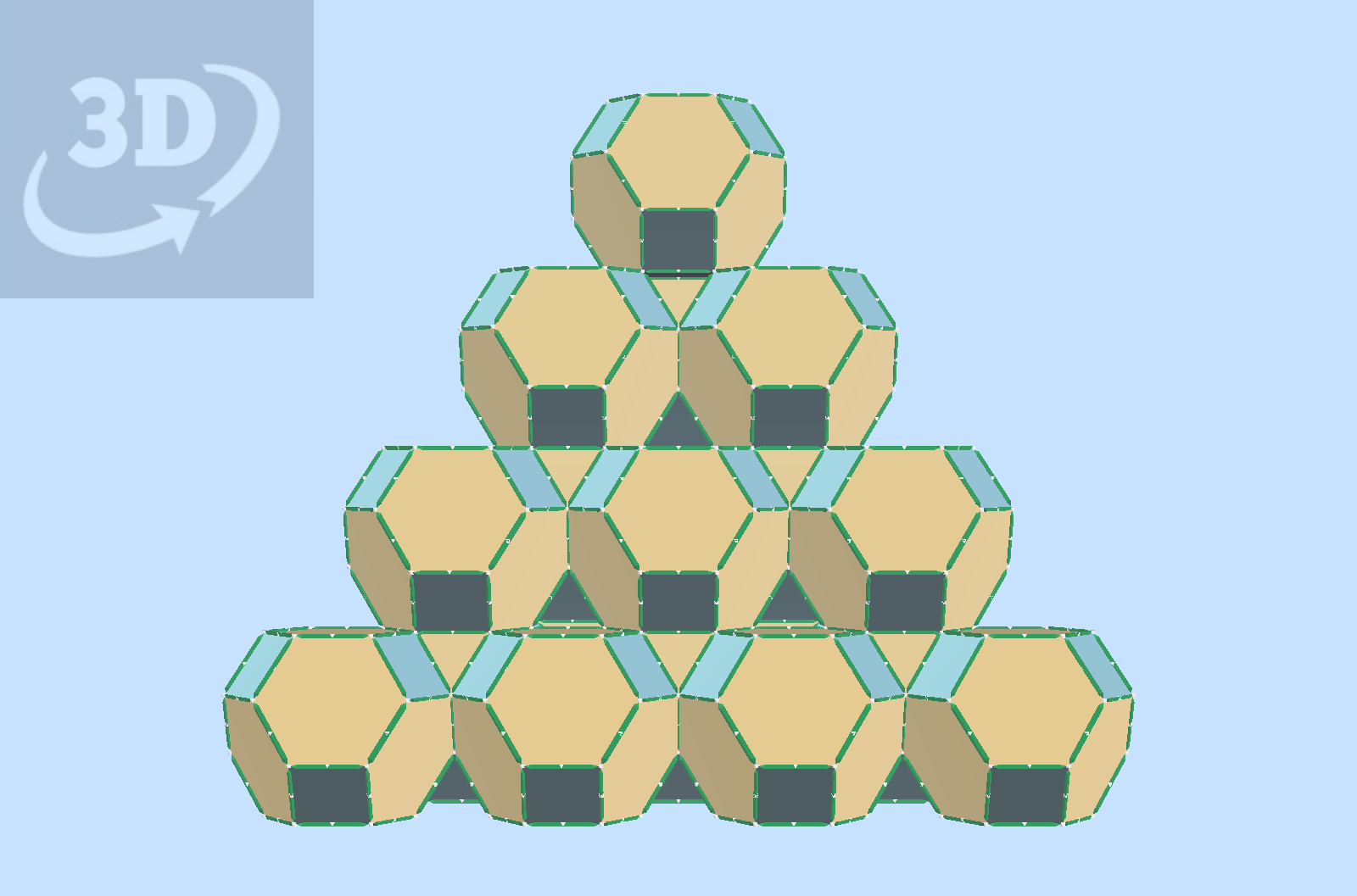
Rather than the familiar “Honeycomb” space-filling array of TO cells that share faces with adjacent cells, one can construct arrays of parallel TOs that are connected to adjacents by shared edges. This shows two ways this can be done. From the bottom cell up, the first mode is to copy the first TO cell to the second position, which is a translation along a green axis, a direction that is parallel to a set of edges of the TO. In this mode, edge sharing is with edges that are part of hexagons, but not squares in the TOs. The second mode is to copy the second cell to a third position, which is a translation along a white axis, a direction that is not parallel to edges of the cell. Edge sharing in this mode is with edges that are parts of squares. While these two types of radial axis are the same length, only the first is an axis of 2-fold rotational symmetry. The second has an appearance of 2-fold symmetry, as a projection. This can be seen by sighting along each of them in turn. It is the symmetries that are inherent in a Truncated Octahedron that makes it a good illustration of how close packing arrays are configured. “Scenes” shows the two modes in a 3-fold group, such as in an HCP array. It is enhanced with a pair of tetrahedra with a shared base triangle, wich can be seen as a mirror plane, The third layer can thus be seen as a reflected copy of the first, with a white edged tetrahedron mirroring the green edged original. It is notable that in both of these modes of edge bonding, the cells are all parallel with the original, and thus all edges are unit lengths within an Oct-Tet lattice, and the spaces between cells can be filled with polyhedra with edges that are likewise Oct-Tet unit lengths.

Here, an array is configured to indicate FCC close packing. Note that all the spaces between cells can be filled with a combination of Cuboctahedra and Truncated Tetrahedra.
Here, an array of edge-connected TO cells is configured to indicate HCP close packing. Note that in this array, some of the spaces between cells can be filled with Cuboctahedra, some only with half Cuboctahedra, and some with Truncated Tetrahedra. Note also that in this array, there is only one axis of 3-fold symmetry, corresponding to the “up” direction in a stack of spheres, such as cannon balls. Hence, Hexagonal Close Packing.

If gravity is disregarded, and cells are considered to be able to bond to adjacents at points of contact in the array, i.e. midpoints of TO edges, it is possible to construct an array with HCP pattern, but in all 4 axes of 3-fold symmetry. This results in a less dense packing than the close packed arrays. This array can be extended, but in chiral forms.